Úvod do neuronových sítí II

4 Sestup a optimalizace gradientu
4.1 Jednoduchý příklad v kódu
4.2 Nákladová funkce
4.3 Sestup gradientu v neuronových sítích
4.4 Příklad dvourozměrného sestupu gradientu
4.5 Zpětné šíření do hloubky
4.6 Šíření do skrytých vrstev
4.7 Vektorizace zpětného šíření algoritmu Finálního sestupu
4.8 Implementace
algoritmu sestupu 9 krokuus

4 Gradient sestup a optimalizace

Jak je uvedeno v části 1, nastavení hodnot váhy, které spojují vrstvy v síti, tvoří trénování systému. Při učení pod dohledem je myšlenkou snížit chybu mezi vstupem a požadovaným výstupem. Pokud tedy máme neuronovou síť s jednou výstupní vrstvou a při určitém vstupu $x$ chceme, aby neuronová síť vydala 2, ale síť ve skutečnosti produkuje 5, jednoduché vyjádření chyby je $abs(2-5) . ) = 3 $. Promatematicky smýšlející by to byla $L^1$ norma chyby (nedělejte si s tím starosti, pokud nevíte, co to je).

Myšlenkou řízeného učení je znát mnoho vstupně-výstupních párů známých dat a měnit váhy na základě těchto vzorků tak, aby se minimalizovalo chybové vyjádření. Tyto vstupně-výstupní páry můžeme specifikovat jako $ \{ (x^{(1)}, y^{(1)}), \ldots, (x^{(m)}, y^{(m)}) \} $ kde $m$ je počet tréninkových vzorků, které máme k dispozici pro trénování vah sítě. Každý z těchto vstupů nebo výstupů může být vektory – to znamená $x^{(1)}$ není nutně jen jedna hodnota, může to být $N$ rozměrná řada hodnot. Řekněme například, že trénujeme neuronovou síť pro detekci spamu – v takovém případě by $x^{(1)}$ mohl být počet všech různých významných slov v e-mailu, např.:

$$ \begin{align} x^{(1)} &= \begin{pmatrix} No. of “prince” \\ No. of “nigeria” \\ No. of “extension” \\ \vdots \\ No. of “mum” \\ No. of “burger” \\ \end{pmatrix} \\ &= \begin{pmatrix} 2 \\ 2 \\ 0 \\ \vdots \\ 0 \\ 1 \\ \end{pmatrix} \end{align} $$

$y^{(1)}$ v tomto případě může být jedna skalární hodnota, buď 1, nebo 0, která určuje, zda je e-mail spam nebo ne. Nebo v jiných aplikacích to může být $K$ rozměrový vektor. Jako příklad řekněme, že máme vstup $x$, který je vektorem obrazových bodů ve stupních šedi fotografie. Máme také výstup $y$, což je 26rozměrný vektor, který pomocí 1 nebo 0 označuje, jaké písmeno abecedy je zobrazeno na fotografii, tj. $(1, 0, \ldots, 0)$ pro a, $ (0, 1, \ldots, 0)$ pro b a tak dále. Tento 26rozměrný výstupní vektor by mohl být použit ke klasifikaci písmen na fotografiích.

Při trénování sítě s těmito páry $(x, y)$ je cílem dosáhnout toho, aby neuronová síť byla stále lepší v předpovídání správného $y$ daného $x$. To se provádí změnou hmotnosti, aby se minimalizovala chyba. Jak víme, jak měnit váhy, když je chyba ve výstupu sítě? Zde přichází vhod koncept gradientního klesání. Zvažte níže uvedený diagram:

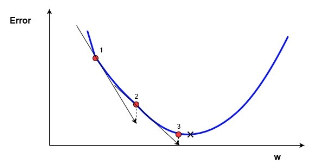  Obrázek 8. Jednoduchý, jednorozměrný gradientní sestup

V tomto diagramu máme modrý graf chyby v závislosti na jediné hodnotě skalární váhy $w$. Minimální možná chyba je označena černým křížkem, ale nevíme, jaká hodnota $w$ tuto minimální chybu udává. Začneme na náhodné hodnotě $w$, což dává chybu označenou červenou tečkou na křivce označené „1“. Musíme změnit $w$ tak, abychom se přiblížili minimální možné chybě, černému křížku. Jeden z nejběžnějších způsobů, jak se k této hodnotě přiblížit, se nazývá gradientní sestup .

Chcete-li pokračovat v této metodě, nejprve se v bodě „1“ vypočte gradient chyby vzhledem k $w$. Pro ty, kteří nevědí, gradient je sklon křivky chyby v tomto bodě. Na obrázku výše je znázorněna černou šipkou, která „proráží“ bod „1“. Gradient také poskytuje směrovou informaci – pokud je kladný vzhledem ke zvýšení $w$, krok tímto směrem povede ke zvýšení chyby. Pokud je záporná vzhledem ke zvýšení $w$ (jak je tomu na výše uvedeném diagramu), krok, který povede ke snížení chyby. Je zřejmé, že chceme udělat krok v $w$, který povede ke snížení chyby. Velikost gradientunebo „strmost“ sklonu udává, jak rychle se v daném bodě mění chybová křivka nebo funkce. Čím vyšší je velikost gradientu, tím rychleji se chyba v daném bodě mění vzhledem k $w$.

Metoda sestupu gradientu používá gradient k informované skokové změně v $w$, aby ji vedl k minimu chybové křivky. Jedná se o iterativní metodu, která zahrnuje více kroků. Pokaždé se hodnota $w$ aktualizuje podle:

$$ \begin{equation} w_{new} = w_{old} – \alpha * \nabla error \end{equation} $$

Zde $w_{new}$ označuje novou pozici $w$, $w_{old}$ označuje aktuální nebo starou pozici $w$, $\nabla error$ je gradient chyby na $w_{old}$ a $\alpha$ je velikost kroku. Velikost kroku $\alpha$ určí, jak rychle řešení konverguje k minimální chybě. Tento parametr je však nutné vyladit – pokud je příliš velký, můžete si představit, že řešení poskakuje po obou stranách minima ve výše uvedeném diagramu. Výsledkem bude optimalizace $w$, která nekonverguje. Jak se tento iterativní algoritmus blíží minimu, gradient nebo změna chyby s každým krokem se sníží. Na výše uvedeném grafu můžete vidět, že čáry přechodu se „vyrovnají“, jakmile se bod řešení přiblíží minimu. Jak se řešení blíží minimální chybě, kvůli klesajícímu gradientu, povede to pouze k malým vylepšením chyby. Když se řešení přiblíží k tomuto „zploštění“ chyby, chceme iterativní proces ukončit. Tento výstup lze provést buď zastavením po určitém počtu iterací, nebo pomocí nějaké „podmínky zastavení“. Tato podmínka zastavení může nastat, když změna chyby klesne pod určitý limit, často nazývanýpřesnost .

4.1 Jednoduchý příklad v kódu

Níže je uveden příklad jednoduché implementace gradientu sestupu v Pythonu pro řešení minima rovnice $f(x) = x^4 – 3x^3 + 2$ převzaté z Wikipedie. Gradient této funkce lze vypočítat analyticky (tj. snadno to uděláme pomocí kalkulu, což s mnoha reálnými aplikacemi neumíme) a je $f'(x) = 4x^3 – 9x^2$ . To znamená, že při každé hodnotě $x$ můžeme vypočítat gradient funkce pomocí jednoduché rovnice. Opět pomocí kalkulu můžeme vědět, že přesné minimum této rovnice je $x = 2,25$ .

x_old = 0 # The value does not matter as long as abs(x_new - x_old) > precision
x_new = 6 # The algorithm starts at x=6
gamma = 0.01 # step size
precision = 0.00001

def df(x):
    y = 4 * x**3 - 9 * x**2
    return y

while abs(x_new - x_old) > precision:
    x_old = x_new
    x_new += -gamma * df(x_old)

print("The local minimum occurs at %f" % x_new)

Tato funkce vytiskne „Místní minimum nastane na 2,249965“, což v rámci přesnosti souhlasí s přesným řešením. Tento kód implementuje algoritmus úpravy hmotnosti, který jsem ukázal výše, a je vidět, že správně našel minimum funkce v rámci dané přesnosti. Toto je velmi jednoduchý příklad sestupu gradientu a nalezení gradientu funguje zcela jinak při trénování neuronových sítí. Hlavní myšlenka však zůstává – zjistíme gradient neuronové sítě a poté postupně upravíme váhy, abychom se přiblížili minimální chybě, kterou se snažíme najít. Dalším rozdílem mezi tímto příkladem spádového sestupu v podobě hračky je to, že vektor hmotnosti je vícerozměrný, a proto musí metoda spádového sestupu hledat minimální bod ve vícerozměrném prostoru.

Způsob, jakým zjišťujeme gradient neuronové sítě, je prostřednictvím známé metody zpětného šíření , o které bude brzy pojednáno. Nejprve se však musíme blíže podívat na chybovou funkci.

4.2 Nákladová funkce

Dříve jsme mluvili o iterativní minimalizaci chyby výstupu neuronové sítě změnou vah v gradientu sestupu. Jak se však ukazuje, existuje matematicky zobecněnější způsob pohledu na věci, který nám umožňuje snížit chyby a zároveň zabránit věcem, jako je přemontování (toto bude více diskutováno v dalších článcích). Tato obecnější formulace optimalizace se točí kolem minimalizace toho, co se nazývá nákladová funkce . Ekvivalentní nákladová funkce jednoho tréninkového páru ($x^z$, $y^z$) v neuronové síti je:

$$ \begin{align} J(w,b,x,y) &= \frac{1}{2} \parallel y^z – h^{(n_l)}(x^z) \parallel ^2 \\ &= \frac{1}{2} \parallel y^z – y_{pred}(x^z) \parallel ^2 \end{align} $$

To ukazuje nákladovou funkci trénovacího vzorku $z_{th}$, kde $h^{(n_l)}$ je výstupem finální vrstvy neuronové sítě, tj. výstupem neuronové sítě. Také jsem reprezentoval $h^{(n_l)}$ jako $y_{pred}$, abych zvýraznil předpověď neuronové sítě dané $x^z$. Dvě svislé čáry představují $L^2$ normu chyby nebo to, co je známé jako chyba součtu čtverců (SSE). SSE je velmi běžný způsob reprezentace chyby systému strojového učení. Místo abychom brali pouze absolutní chybu $abs(y_{pred}(x^z) – y^z)$, použijeme druhou mocninu chyby. Existuje mnoho důvodů, proč se SSE často používá, o kterých zde nebudeme hovořit – stačí říci, že jde o velmi běžný způsob reprezentace chyb ve strojovém učení.

Všimněte si, že formulace pro funkci nákladů výše je pro jeden $(x,y)$ tréninkový pár. Chceme minimalizovat nákladovou funkci u všech našich $ m$ tréninkových párů. Proto chceme najít minimální *střední čtvercovou chybu* (MSE) přes všechny trénovací vzorky:

$$ \begin{align} J(w,b) &= \frac{1}{m} \sum_{z=0}^m \frac{1}{2} \parallel y^z – h^{(n_l)}(x^z) \parallel ^2 \\ &= \frac{1}{m} \sum_{z=0}^m J(W, b, x^{(z)}, y^{(z)}) \end{align} $$

Jak tedy použijete výše uvedenou nákladovou funkci $J$ k trénování vah naší sítě? Použití gradientního klesání a zpětného šíření. Nejprve se podívejme na gradientní sestup blíže v neuronových sítích.

4.3 Gradient sestup v neuronových sítích

Gradientní sestup pro každou váhu $w_{(ij)}^{(l)}$ a každou odchylku $b_i^{(l)}$ v neuronové síti vypadá takto:

$$ \begin{align} w_{ij}^{(l)} &= w_{ij}^{(l)} – \alpha \frac{\partial}{\partial w_{ij}^{(l)}} J(w,b) \\ b_{i}^{(l)} &= b_{i}^{(l)} – \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(w,b) \end{align} $$

V zásadě je výše uvedená rovnice podobná dříve uvedenému algoritmu sestupu gradientu: $w_{new} = w_{old} – \alpha * \nabla error$. Chybí nový a starý index, ale hodnoty na levé straně rovnice jsou nové a hodnoty na pravé straně jsou staré . Opět máme iterační proces, kdy se váhy aktualizují v každé iteraci, tentokrát na základě nákladové funkce $J(w,b)$.

Hodnoty $\frac{\partial}{\partial w_{ij}^{(l)}}$ a $\frac{\partial}{\partial b_{i}^{(l)}}$ jsou částečné derivace funkce nákladů na jeden vzorek na základě hodnot hmotnosti. Co to znamená? Připomeňme si, že u výše uvedeného jednoduchého příkladu sestupu s gradientem závisí každý krok na sklonu členu chyba/náklad s ohledem na váhy. Další slovo pro sklon nebo sklon je derivace . Normální derivace má zápis $\frac{d}{dx}$. Pokud je $x$ v tomto případě vektor, pak taková derivace bude také vektor, zobrazující gradient ve všech rozměrech $x$.

4.4 Příklad dvourozměrného gradientu

Vezměme si příklad standardního problému sestupu dvourozměrného gradientu. Níže je schéma iterativního dvourozměrného gradientového sestupu:

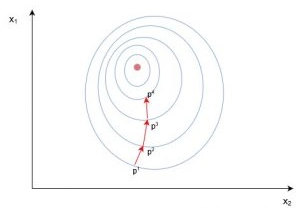Obrázek 9. Dvourozměrný gradient sestup

Modré čáry ve výše uvedeném diagramu jsou obrysové čáry nákladové funkce – označující regiony s chybovou hodnotou, která je přibližně stejná. Jak lze pozorovat v diagramu výše, každý krok ($p_1 \to p_2 \to p_3$) v sestupu gradientu zahrnuje gradient nebo derivaci, která je šipkou/vektorem. Tento vektor zahrnuje oba rozměry $[x_1, x_2]$, protože řešení směřuje k minimu ve středu. Takže například derivace ohodnocená na $p_1$ může být $\frac {d}{dx} = [2.1, 0.7]$, kde derivace je vektor označující dva směry. Částečné _derivace $\frac {\partial}{\partial x_1}$ by v tomto případě byl skalární $\to [2.1]$ – jinými slovy je to gradient pouze v jednom směru prohledávaného prostoru ($x_1$) . Při sestupu s gradientem se často stává, že se vypočítá částečná derivace všech možných směrů hledání a poté se „shromáždí“ a určí se nový, úplný směr kroku.

V neuronových sítích nemáme jednoduchou nákladovou funkci, kde bychom mohli snadno vyhodnotit gradient, jako jsme to udělali v našem příkladu sestupu gradientu hraček ($f(x) = x^4 – 3x^3 + 2$). Ve skutečnosti jsou věci ještě složitější. I když můžeme porovnat výstup neuronové sítě s naší očekávanou trénovací hodnotou $y^{(z)}$ a reálně se podívat na to, jak by změna vah výstupní vrstvy změnila nákladovou funkci pro vzorek (tj. výpočet gradientu ), jak to proboha uděláme pro všechny skryté vrstvy sítě?

Odpovědí na to je metoda zpětného šíření. Tato metoda nám umožňuje „sdílet“ nákladovou funkci nebo chybu se všemi váhami v síti – nebo jinými slovy, umožňuje nám určit, jak velká část chyby je způsobena danou váhou.

4.5 Zpětné šíření do hloubky

V této části se trochu ponořím do matematiky. Pokud se bojíte matematiky, jak funguje backpropagation, pak může být nejlepší tuto část přeskočit. Následující část vám ukáže, jak implementovat backpropagation v kódu – takže pokud chcete přeskočit rovnou k použití této metody, klidně přeskočte zbytek této části. Pokud vám však nevadí trochu matematiky, doporučuji vám přejít na konec této části, protože vám poskytne dobrou hloubku porozumění při trénování neuronových sítí. To bude neocenitelné pro pochopení některých klíčových myšlenek v hlubokém učení, spíše než být pouhým cruncherem kódu, který ve skutečnosti nerozumí tomu, jak kód funguje.

Nejprve si připomeňme některé základní rovnice z oddílu 3 pro následující třívrstvou neuronovou síť:

Obrázek 10. Třívrstvá neuronová síť (opět)

Výstup této neuronové sítě lze vypočítat:

$$ \begin{equation} h_{W,b}(x) = h_1^{(3)} = f(w_{11}^{(2)}h_1^{(2)} + w_{12}^{(2)} h_2^{(2)} + w_{13}^{(2)} h_3^{(2)} + b_1^{(2)}) \end{equation} $$

Výše uvedené můžeme také zjednodušit na $h_1^{(3)} = f(z_1^{(2)})$ definováním $z_1^{(2)}$ jako:

$$ z_{1}^{(2)} = w_{11}^{(2)}h_1^{(2)} + w_{12}^{(2)} h_2^{(2)} + w_{13}^{(2)} h_3^{(2)} + b_1^{(2)} $$

Řekněme, že chceme zjistit, jak velkou má změna váhy $w_{12}^{(2)}$ na nákladové funkci $J$. Toto má vyhodnotit $\frac {\partial J}{\partial w_{12}^{(2)}}$. K tomu musíme použít něco, co se nazývá řetězová funkce:

$$ \frac {\partial J}{\partial w_{12}^{(2)}} = \frac {\partial J}{\partial h_1^{(3)}} \frac {\partial h_1^{(3)}}{\partial z_1^{(2)}} \frac {\partial z_1^{(2)}}{\partial w_{12}^{(2)}} $$

Když se podíváte na výrazy vpravo – čitateli a „vyruší“ jmenovatele stejným způsobem jako $\frac {2}{5} \frac {5}{2} = \frac {2}{2} = 1 $. Proto můžeme zkonstruovat $\frac {\partial J}{\partial w_{12}^{(2)}}$ spojením několika parciálních derivací (které jsou naštěstí docela snadné). Začněme s $\frac {\partial z_1^{(2)}}{\partial w_{12}^{(2)}}$:

$$ \begin{align} \frac {\partial z_1^{(2)}}{\partial w_{12}^{(2)}} &= \frac {\partial}{\partial w_{12}^{(2)}} (w_{11}^{(1)}h_1^{(2)} + w_{12}^{(1)} h_2^{(2)} + w_{13}^{(1)} h_3^{(2)} + b_1^{(1)})\\ &= \frac {\partial}{\partial w_{12}^{(2)}} (w_{12}^{(1)} h_2^{(2)})\\ &= h_2^{(2)} \end{align} $$

Částečná derivace $z_1^{(2)}$ vzhledem k $w_{12}^{(2)}$ funguje pouze s jedním výrazem v závorce, $w_{12}^{(1)} h_2^{ (2)}$, protože všechny ostatní výrazy se v případě $w_{12}^{(2)}$ vůbec neliší. Derivace konstanty je 1, proto $\frac {\partial}{\partial w_{12}^{(2)}} (w_{12}^{(1)} h_2^{(2)})$ se zhroutí na pouhých $h_2^{(2)}$, což je jednoduše výstup druhého uzlu ve vrstvě 2.

Další parciální derivace v řetězci je $ \frac {\partial h_1^{(3)}}{\partial z_1^{(2)}} $, což je parciální derivace aktivační funkce $h_1^{ (3)}$ výstupní uzel. Vzhledem k požadavku na možnost odvodit tuto derivaci musí být aktivační funkce v neuronových sítích diferencovatelné. Pro běžnou esovitou aktivační funkci (zobrazenou v sekci 2.1 ) je derivace:

$$ \frac {\partial h}{\partial z} = f'(z) = f(z)(1-f(z)) $$

Kde $f(z)$ je aktivační funkce. Zatím je to dobré – teď musíme vyřešit, jak naložit s prvním členem $\frac {\partial J}{\partial h_1^{(3)}}$. Pamatujte si, že $J(w,b,x,y)$ je střední čtvercová funkce ztráty chyb, která vypadá (pro náš případ):

$$ J(w,b,x,y) = \frac{1}{2} \parallel y_1 – h_1^{(3)}(z_1^{(2)}) \parallel ^2 $$

Zde $y_1$ je cíl školení pro výstupní uzel. Opět pomocí řetězového pravidla:

$$ \begin{align} &Let\ u = \parallel y_1 – h_1^{(3)}(z_1^{(2)}) \parallel\ and\ J = \frac {1}{2} u^2\\ &Using\ \frac {\partial J}{\partial h} = \frac {\partial J}{\partial u} \frac {\partial u}{\partial h}:\\ &\frac {\partial J}{\partial h} = -(y_1 – h_1^{(3)}) \end{align} $$

Nyní jsme tedy přišli na to, jak vypočítat $\frac {\partial J}{\partial w_{12}^{(2)}}$, alespoň pro váhy spojující výstupní vrstvu. Než přejdeme k jakýmkoli skrytým vrstvám (tj. vrstvě 2 v našem příkladu), zavedeme některá zjednodušení pro zpřísnění našeho zápisu a zavedeme $\delta$:

$$ \delta_i^{(n_l)} = -(y_i – h_i^{(n_l)})\cdot f^\prime(z_i^{(n_l)}) $$

Kde $i$ je číslo uzlu výstupní vrstvy. V našem vybraném příkladu je pouze jedna taková vrstva, proto $i=1$ v tomto případě vždy. Nyní můžeme napsat úplnou derivaci nákladové funkce jako:

$$ \begin{align} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b,x, y) &= h^{(l)}_j \delta_i^{(l+1)} \\ \end{align} $$

Kde pro výstupní vrstvu v našem případě $l$ = 2 a $i$ zůstává číslem uzlu.

4.6 Propagace do skrytých vrstev

Jak je to s podáváním závaží do skrytých vrstev (v našem případě vrstva 2)? Pro váhy spojující výstupní vrstvu dávala derivace $\frac {\partial J}{\partial h} = -(y_i – h_i^{(n_l)})$ smysl, protože nákladovou funkci lze přímo vypočítat porovnáním výstupní vrstvu k tréninkovým datům. Výstup skrytých uzlů však žádnou takovou přímou referenci nemá, spíše jsou spojeny s nákladovou funkcí pouze prostřednictvím zprostředkujících vah a potenciálně dalších vrstev uzlů. Jak můžeme najít variaci v nákladové funkci od změn k vahám uloženým hluboko v neuronové síti? Jak již bylo zmíněno, používáme metodu zpětného šíření .

Nyní, když jsme udělali tvrdou práci pomocí pravidla řetězu, nyní zvolíme grafickější přístup. Termín, který se musí šířit sítí zpět, je termín $\delta_i^{(n_l)}$, protože jde o konečné spojení sítě s nákladovou funkcí. A co uzel j ve druhé vrstvě (skrytá vrstva)? Jak to přispívá k $\delta_i^{(n_l)}$ v naší testovací síti? Přispívá váhou $w_{ij}^{(2)}$ – viz diagram níže pro případ $j=1$ a $i=1$.

Obrázek 11. Jednoduchá ilustrace zpětného šíření

Jak je vidět shora, výstupní vrstva $\delta$ je sdělena skrytému uzlu vahou spojení. V případě, že existuje pouze jeden uzel výstupní vrstvy, je zobecněná skrytá vrstva $\delta$ definována jako:

$$\delta_j^{(l)} = \delta_1^{(l+1)} w_{1j}^{(l)}\ f^\prime(z_j)^{(l)}$$

Kde $j$ je číslo uzlu ve vrstvě $l$. A co případ, kdy existuje více výstupních uzlů? V tomto případě se pro výpočet $\delta_j^{(l)}$ použije vážený součet všech oznámených chyb, jak je znázorněno na obrázku níže:

Obrázek 12. Ilustrace zpětného šíření s více výstupy

Jak je patrné z výše uvedeného, ​​každá hodnota $\delta$ z výstupní vrstvy je zahrnuta do součtu použitého k výpočtu $\delta_1^{(2)}$, ale každý výstup $\delta$ je vážen podle příslušné $w_{i1}^{(2)}$ hodnotu. Jinými slovy, uzel 1 ve vrstvě 2 přispívá k chybě tří výstupních uzlů, proto naměřená chyba (nebo hodnota nákladové funkce) v každém z těchto uzlů musí být „předána zpět“ hodnotě $\delta$ pro tento uzel. . Nyní můžeme vytvořit zobecněný výraz pro hodnoty $\delta$ pro uzly ve skrytých vrstvách:

$$\delta_j^{(l)} = (\sum_{i=1}^{s_{(l+1)}} w_{ij}^{(l)} \delta_i^{(l+1)} )\ f^\prime(z_j^{(l)})$$

Kde $j$ je číslo uzlu ve vrstvě $l$ a $i$ je číslo uzlu ve vrstvě $l+1$ (což je stejný zápis, jaký jsme použili od začátku). Hodnota $s_{(l+1)}$ je počet uzlů ve vrstvě $(l+1)$.

Nyní tedy víme, jak vypočítat: $$\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b,x, y) = h^{(l)}_j \ delta_i^{(l+1)}$$, jak je uvedeno výše. A co zkreslení váhy? Nebudu je odvozovat jako u normálních vah v zájmu úspory času/místa. Čtenář by však neměl mít příliš mnoho problémů po stejných krocích s použitím pravidla řetězce, aby dospěl k:

$$\frac{\partial}{\částečné b_{i}^{(l)}} J(W,b,x,y) = \delta_i^{(l+1)}$$

Skvělé – takže nyní víme, jak provést náš původní problém sestupu gradientu pro neuronové sítě:

$$ \begin{align} w_{ij}^{(l)} &= w_{ij}^{(l)} – \alpha \frac{\partial}{\partial w_{ij}^{(l)}} J(w,b) \\ b_{i}^{(l)} &= b_{i}^{(l)} – \alpha \frac{\partial}{\partial b_{i}^{(l) )}} J(w,b) \end{align} $$

Abychom však provedli tento gradientní nácvik sestupu závaží, museli bychom se uchýlit ke smyčkám uvnitř smyček. Jak bylo uvedeno dříve v sekci 3.4 tohoto tutoriálu pro neuronové sítě, provádění takových výpočtů v Pythonu pomocí smyček je pro velké sítě pomalé. Proto musíme vymyslet, jak takové výpočty vektorizovat, což ukáže další část.

4.7 Vektorizace zpětného šíření

Abychom zvážili, jak vektorizovat výpočty gradientu sestupu v neuronových sítích, podívejme se nejprve na naivní vektorizovanou verzi gradientu nákladové funkce ( varování : toto ještě není ve správné podobě!):

$$ \begin{align} \frac{\partial J}{\partial W^{(l)}} &= h^{(l)} \delta^{(l+1)}\\ \frac{\partial J }{\partial b^{(l)}} &= \delta^{(l+1)} \end{align} $$

Nyní se podívejme, jaký prvek výše uvedených rovnic. Jak $h^{(l)}$ vypadá? Docela jednoduché, jen vektor $(s_l \krát 1)$, kde $s_l$ je počet uzlů ve vrstvě $l$. Jak vypadá násobení $h^{(l)} \delta^{(l+1)}$? Protože víme, že $\alpha \times \frac{\partial J}{\partial W^{(l)}}$ musí mít stejnou velikost matice váhy $W^{(l)}$, vědět, že výsledek $h^{(l)} \delta^{(l+1)}$ musí mít také stejnou velikost jako matice váhy pro vrstvu $l$. Jinými slovy, musí mít velikost $(s_{l+1} \times s_{l})$.

Víme, že $\delta^{(l+1)}$ má rozměr $(s_{l+1} \krát 1)$ a že $h^{(l)}$ má rozměr $(s_l \ krát 1) $. Pravidla násobení matic ukazují, že matice dimenze $(\mathbf n \times m)$ vynásobená maticí dimenze $(o \times \mathbf p)$ bude mít matici součinu o velikosti $(\mathbf n \ krát \mathbf p)$. Pokud provedeme přímé násobení mezi $h^{(l)}$ a $\delta^{(l+1)}$, počet sloupců prvního vektoru (tj. 1 sloupec) se nebude rovnat počtu řádků druhého vektoru (tj. 3 řádky), proto nemůžeme provést správné násobení matice. Jediný způsob, jak můžeme získat správný výsledek velikosti $(s_{l+1} \krát s_{l})$, je použití maticové transpozice. Transpozice zamění rozměry matice kolem např. vektoru o velikosti $(s_l \times 1)$ se stane vektorem velikosti $(1 \times s_l)$ a bude označena horním indexem $T$. Proto můžeme provést následující:

$$\delta^{(l+1)} (h^{(l)})^T = (s_{l+1} \krát 1) \krát (1 \krát s_l) = (s_{l+1 } \times s_l)$$

Jak je vidět níže, pomocí operace transpozice můžeme dospět k požadovanému výsledku.

Konečná vektorizace, kterou lze provést, je během váženého sčítání chyb v kroku zpětného šíření:

$$\delta_j^{(l)} = (\sum_{i=1}^{s_{(l+1)}} w_{ij}^{(l)} \delta_i^{(l+1)} )\ f^\prime(z_j^{(l)}) = \left((W^{(l)})^T \delta^{(l+1)}\right) \bullet f'(z^ {(l)})$$

Symbol $\bullet$ ve výše uvedeném označuje násobení prvku po prvku (nazývané Hadamardův součin), nikoli násobení matice. Všimněte si, že maticové násobení $\left((W^{(l)})^T \delta^{(l+1)}\right)$ provede nezbytný součet vah a hodnot $\delta$ – čtenář může ověřit, že tomu tak je.

4.8 Implementace kroku gradientu klesání

Jak nyní integrujeme tuto novou vektorizaci do kroků gradientu sestupu našeho algoritmu, který bude brzy zakódován? Nejprve se musíme znovu podívat na celkovou nákladovou funkci, kterou se snažíme minimalizovat (nejen na nákladovou funkci vzorek po vzorku uvedenou v předchozí rovnici):

$$ \begin{align} J(a,b) &= \frac{1}{m} \sum_{z=0}^m J(a, b, x^{(z)}, y^{(z) }) \end{align} $$

Jak můžeme pozorovat, funkce celkových nákladů je průměrem všech výpočtů nákladové funkce vzorek po vzorku. Pamatujte také na výpočet gradientu sestupu (zobrazení verze po prvku spolu s vektorizovanou verzí):

$$ \begin{align} w_{ij}^{(l)} &= w_{ij}^{(l)} – \alpha \frac{\partial}{\partial w_{ij}^{(l)}} J(w,b)\\ W^{(l)} &= W^{(l)} – \alpha \frac{\partial}{\partial W^{(l)}} J(w,b) \\ &= W^{(l)} – \alpha \left[\frac{1}{m} \sum_{z=1}^{m} \frac {\partial}{\partial W^{(l )}} J(a,b,x^{(z)},y^{(z)}) \right]\\ \end{align} $$

To znamená, že když procházíme našimi cvičnými vzorky nebo dávkami, musíme mít výraz, který shrnuje parciální derivace jednotlivých výpočtů funkce nákladů na vzorky. Tento výraz shromáždí všechny hodnoty pro výpočet průměru. Nazvěme tento „sčítací“ termín $\Delta W^{(l)}$. Podobně lze ekvivalentní člen zkreslení nazvat $\Delta b^{(l)}$. Proto při každé vzorové iteraci konečného trénovacího algoritmu musíme provést následující kroky:

$$ \begin{align} \Delta W^{(l)} &= \Delta W^{(l)} + \frac {\partial}{\partial W^{(l)}} J(a,b,x ^{(z)},y^{(z)})\\ &= \Delta W^{(l)} + \delta^{(l+1)} (h^{(l)})^T \\ \Delta b^{(l)} &= \Delta b^{(1)} + \delta^{(l+1)} \end{align} $$

Provedením výše uvedených operací při každé iteraci pomalu vytvoříme výše zmíněný součet $\sum_{z=1}^{m} \frac {\partial}{\partial W^{(l)}} J(w, b,x^{(z)},y^{(z)})$ (a totéž pro $b$). Jakmile projdou všechny vzorky a sečtou se hodnoty $\Delta$, aktualizujeme parametry hmotnosti:

$$ \begin{align} W^{(l)} &= W^{(l)} – \alpha \left[\frac{1}{m} \Delta W^{(l)} \right] \\ b ^{(l)} &= b^{(l)} – \alpha \left[\frac{1}{m} \Delta b^{(l)}\right] \end{align} $$

4.9 Algoritmus konečného sestupu gradientu

Takže ne, konečně jsme se dostali do bodu, kdy můžeme specifikovat celé trénování gradientu sestupu založené na backpropagation našich neuronových sítí. Udělalo to několik kroků, aby se to ukázalo, ale doufejme, že to bylo poučné. Konečný algoritmus zpětného šíření je následující:

Náhodně inicializujte váhy pro každou vrstvu $W^{(l)}$
Zatímco iterace < iterační limit:
1. Nastavte $\Delta W$ a $\Delta b$ na nulu
2. Pro vzorky 1 až m:
a. Proveďte průchod vpřed skrz všechny $n_l$ vrstvy. Uložte výstupy aktivační funkce $h^{(l)}$
b. Vypočítejte hodnotu $\delta^{(n_l)}$ pro výstupní vrstvu
c. Použijte backpropagation k výpočtu hodnot $\delta^{(l)}$ pro vrstvy 2 až $n_l-1$
d. Aktualizujte $\Delta W^{(l)}$ a $\Delta b^{(l)}$ pro každou vrstvu
3. Proveďte krok sestupu s přechodem pomocí:

$W^{(l)} = W^{(l)} – \alpha \left[\frac{1}{m} \Delta W^{(l)} \right]$
$b^{(l) } = b^{(l)} – \alpha \left[\frac{1}{m} \Delta b^{(l)}\right]$

Jak je uvedeno ve výše uvedeném algoritmu, opakovali bychom rutinu sestupu gradientu, dokud nebudeme rádi, že funkce průměrných nákladů dosáhla minima. V tuto chvíli je naše síť natrénovaná a (v ideálním případě) připravena k použití.

Další část tohoto tutoriálu o neuronových sítích ukáže, jak implementovat tento algoritmus pro trénování neuronové sítě, která rozpoznává ručně psané číslice.