Matematický úvod do problematiky neuronových sítí. Struktura, průchody, uzly, sestavení struktury.
V tomto tutoriálu jsou představeny některé koncepty, kód a matematiku, které vám umožní vytvořit a pochopit jednoduchou neuronovou síť. Některé výukové programy se zaměřují pouze na kód a přeskakují matematiku – to však brání porozumění. Kód je v Pythonu, takže bude přínosné, pokud budete mít základní znalosti o tom, jak Python funguje.
1 Co jsou umělé neuronové sítě?
2 Struktura ANN
2.1 Umělý neuron
2.2 Uzly
2.3 Předpojatost
2.4 Sestavení struktury
2.5 Zápis
3 Průchod
zpětné vazby 3.1 Příklad předávání zpětné vazby
3.2 Náš první pokus o funkci předávání zpětné vazby
3.3 Efektivnější implementace
3.4 Vektorizace v neuronových sítích
3.5 Násobení matic
1 Co jsou umělé neuronové sítě?
Umělé neuronové sítě (ANN) jsou softwarové implementace neuronální struktury našeho mozku. Nemusíme mluvit o složité biologii našich mozkových struktur, ale stačí říci, že mozek obsahuje neurony , které jsou něco jako organické spínače. Ty mohou měnit svůj výstupní stav v závislosti na síle jejich elektrického nebo chemického vstupu. Neuronová síť v mozku člověka je obrovsky propojená síť neuronů, kde výstup jakéhokoli daného neuronu může být vstupem pro tisíce dalších neuronů. K učení dochází opakovanou aktivací určitých nervových spojení nad ostatními, což tato spojení posiluje. Díky tomu s větší pravděpodobností dosáhnou požadovaného výsledku při zadaném vstupu. Toto učení zahrnuje zpětnou vazbu– když dojde k požadovanému výsledku, nervová spojení způsobující tento výsledek se posílí.
Umělé neuronové sítě se snaží toto chování mozku zjednodušit a napodobit. Mohou být trénováni pod dohledem nebo bez dozoru . V ANN pod dohledem je síť trénována poskytováním přizpůsobených vzorků vstupních a výstupních dat se záměrem přimět ANN, aby poskytovala požadovaný výstup pro daný vstup. Příkladem je e-mailový spamový filtr – vstupními trénovacími daty by mohl být počet různých slov v těle e-mailu a výstupními trénovacími daty by byla klasifikace toho, zda byl e-mail skutečně spam či nikoli. . Pokud neuronovou sítí prochází mnoho příkladů e-mailů, umožňuje to síti učit se podle jakých vstupních dat je pravděpodobné, že e-mail je spam nebo ne. Toto učení probíhá při nastavování vah spojení ANN, ale o tom bude pojednáno dále v další části.
Učení bez dozoru v ANN je pokus přimět ANN, aby „pochopila“ strukturu poskytovaných vstupních dat „sama od sebe“. Tento typ ANN nebude v tomto příspěvku diskutován.
2 Struktura ANN
2.1 Umělý neuron
Biologický neuron je simulován v ANN aktivační funkcí. V klasifikačních úlohách (např. identifikace spamových e-mailů) musí mít tato aktivační funkce charakteristiku „zapnout“ – jinými slovy, jakmile je vstup větší než určitá hodnota, výstup by měl změnit stav, tj. z 0 na 1, od -1 až 1 nebo od 0 do >0. To simuluje „zapnutí“ biologického neuronu. Běžnou aktivační funkcí, která se používá, je sigmoidní funkce:
$$ \begin{equation*} f(z) = \frac{1}{1+exp(-z)} \end{equation*} $$
Což vypadá takto:
import matplotlib.pylab as plt
import numpy as np
x = np.arange(-8, 8, 0.1)% 0Af = 1 / (1 + np.exp(-x))
plt.plot(x, f)
plt.xlabel('x')
plt .ylabel('f(x)')
plt.show()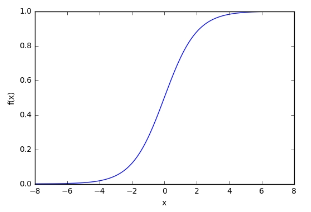
Jak je vidět na obrázku výše, funkce je „aktivovaná“, tj. pohybuje se z 0 na 1, když je vstup x větší než určitá hodnota. Sigmoidní funkce však není kroková, hrana je „měkká“ a výstup se nemění okamžitě. To znamená, že existuje derivace funkce a to je důležité pro trénovací algoritmus, který je více diskutován v části 4.
2.2 Uzly
Jak již bylo zmíněno dříve, biologické neurony jsou propojené hierarchické sítě, přičemž výstupy některých neuronů jsou vstupy pro jiné. Tyto sítě můžeme reprezentovat jako spojené vrstvy uzlů. Každý uzel přijímá více vážených vstupů, aplikuje aktivační funkci na sčítání těchto vstupů a přitom generuje výstup. Rozeberu to dále, ale abyste si to usnadnili, zvažte níže uvedený diagram:
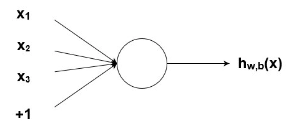Obrázek 2. Uzel se vstupy
Kruh na obrázku výše představuje uzel. Uzel je „sídlem“ aktivační funkce a přijímá vážené vstupy, sečte je a poté je vkládá do aktivační funkce. Výstup aktivační funkce je ve výše uvedeném diagramu znázorněn jako h . Poznámka: uzel , jak jsem ukázal výše, se v některé literatuře také nazývá perceptron.
A co tato myšlenka „váhy“, která byla zmíněna? Váhy jsou reálná čísla (tj. ne binární 1s nebo 0s), která se vynásobí vstupy a pak sečtou v uzlu. Jinými slovy, vážený vstup do výše uvedeného uzlu by byl:
$$ \begin{equation*} x_1w_1 + x_2w_2 + x_3w_3 + b \end{equation*} $$
Hodnoty $w_i$ jsou zde váhy (prozatím ignorujte $b$). O čem jsou tyto závaží? Jsou to proměnné, které se mění během procesu učení a spolu se vstupem určují výstup uzlu. $b$ je váha prvku zkreslení +1 – zahrnutí tohoto zkreslení zvyšuje flexibilitu uzlu, což je nejlépe demonstrováno na příkladu.
2.3 Předpojatost
Vezměme si extrémně jednoduchý uzel s pouze jedním vstupem a jedním výstupem:
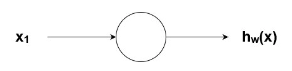Obrázek 2. Jednoduchý uzel
Vstup do aktivační funkce uzlu je v tomto případě jednoduše $x_1w_1$. Co udělá změna $w_1$ v této jednoduché síti?
w1 = 0.5
w2 = 1.0
w3 = 2.0
l1 = 'w = 0.5'
l2 = 'w = 1.0'
l3 = 'w = 2.0'
for w, l in [(w1 , l1), (w2, l2), (w3, l3)]:
f = 1 % 2F (1 + np.exp(-x*w))
plt.plot(x, f, label=l)
plt.xlabel( 'x')
plt.ylabel('h_w(x)')
plt.legend(loc=2)
plt.show()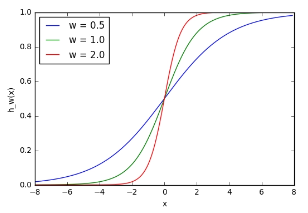
Obrázek 4. Účinek seřizovacích závaží
Zde vidíme, že změnou váhy se mění strmost výstupu sigmoidní aktivační funkce, což je samozřejmě užitečné, pokud chceme modelovat různé síly vztahů mezi vstupními a výstupními proměnnými. Co když však chceme, aby se výstup měnil pouze tehdy, když je x větší než 1? Zde přichází na řadu zkreslení – uvažujme stejnou síť se vstupem zkreslení:
Obrázek 5. Účinek zkreslení
w = 5.0
b1 = -8.0
b2 = 0.0
b3 = 8.0
l1 =% 20'b = -8.0'
l2 = 'b = 0.0'
l3 = 'b = 8.0'
for b , l in [(b1, l1), (b2, l2), (b3, l3)]:
% 20 f = 1 / (1 + np.exp(-(x*w+b)))
plt.plot(x , f, label=l)
plt.xlabel('x')
plt.ylabel('h_wb(x)')
plt.legend(loc=2)
plt.show()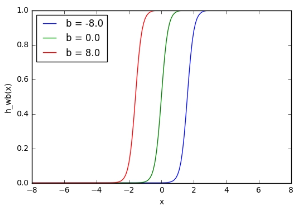
Obrázek 6. Účinek úprav zkreslení
V tomto případě byla hodnota $w_1$ zvýšena, aby simulovala přesněji definovanou funkci „zapnutí“. Jak vidíte, změnou „váhy“ $b$ můžete změnit, kdy se uzel aktivuje. Přidáním členu zkreslení tedy můžete přimět uzel simulovat obecnou funkci if , tj. if (x > z) then 1 else 0 . Bez výrazu zkreslení nemůžete měnit z v tom, že příkaz if bude vždy uvíznutý kolem 0. To je samozřejmě velmi užitečné, pokud se snažíte simulovat podmíněné vztahy.
2.4 Sestavení konstrukce
Doufejme, že předchozí vysvětlení vám poskytla dobrý přehled o tom, jak daný uzel/neuron/perceptron v neuronové síti funguje. Jak však pravděpodobně víte, v plnohodnotné neuronové síti existuje mnoho takových propojených uzlů. Tyto struktury mohou mít nespočet různých forem, ale nejběžnější jednoduchá struktura neuronové sítě se skládá ze vstupní vrstvy, skryté vrstvy a výstupní vrstvy. Příklad takové struktury lze vidět níže:
Obrázek 10. Třívrstvá neuronová síť
Tři vrstvy sítě jsou vidět na obrázku výše – Vrstva 1 představuje vstupní vrstvu , odkud do sítě vstupují externí vstupní data. Vrstva 2 se nazývá skrytá vrstva , protože tato vrstva není součástí vstupu ani výstupu. Poznámka: neuronové sítě mohou mít mnoho skrytých vrstev, ale v tomto případě jsem pro jednoduchost zahrnul jednu. A konečně, vrstva 3 je výstupní vrstvou . Můžete pozorovat mnoho spojení mezi vrstvami, zejména mezi vrstvou 1 (L1) a vrstvou 2 (L2). Jak je vidět, každý uzel v L1 má spojení se všemi uzly v L2. Podobně pro uzly v L2 až jeden výstupní uzel L3. Každé z těchto spojení bude mít přiřazenou váhu.
2.5 Zápis
Níže uvedená matematika vyžaduje poměrně přesný zápis, abychom věděli, o čem mluvíme. Zápis, který zde používám, je podobný zápisu použitému ve výukovém programu hlubokého učení ve Stanfordu. V následujících rovnicích je každá z těchto vah označena následujícím zápisem: ${w_{ij}}^{(l)}$. $i$ odkazuje na číslo uzlu spojení ve vrstvě $l+1$ a $j$ odkazuje na číslo uzlu spojení ve vrstvě $l$. Věnujte zvláštní pozornost této objednávce. Takže pro spojení mezi uzlem 1 ve vrstvě 1 a uzlem 2 ve vrstvě 2 by zápis váhy byl ${w_{21}}^{(1)}$. Tento zápis se může zdát trochu zvláštní, protože byste očekávali, že *i* a *j* odkazují na čísla uzlů ve vrstvách $l$ a $l+1$ (tj. ve směru vstupu k výstupu), spíše než opak. Tento zápis však dává větší smysl, když přidáte zkreslení.
Jak můžete vidět na obrázku výše – předpětí (+1) je spojeno s každým z uzlů v následující vrstvě. Takže zkreslení ve vrstvě 1 je spojeno se všemi uzly ve vrstvě dva. Protože zkreslení není skutečným uzlem s aktivační funkcí, nemá žádné vstupy (vždy vydává hodnotu +1). Zápis váhy zkreslení je ${b_i}^{(l)}$, kde *i* je číslo uzlu ve vrstvě $l+1$ – stejné jako pro zápis normální váhy ${w_{21 }}^{(1)}$. Takže váha na spojení mezi předpětím ve vrstvě 1 a druhým uzlem ve vrstvě 2 je dána ${b_2}^{(1)}$.
Pamatujte, že tyto hodnoty – ${w_{ji}}^{(1)}$ a ${b_i}^{(l)}$ – všechny je třeba vypočítat ve fázi školení ANN.
Nakonec výstupní zápis uzlu je ${h_j}^{(l)}$, kde $j$ označuje číslo uzlu ve vrstvě $l$ sítě. Jak lze pozorovat ve výše uvedené třívrstvé síti, výstup uzlu 2 ve vrstvě 2 má zápis ${h_2}^{(2)}$.
Nyní, když máme notaci vyřešenou, je nyní čas podívat se, jak vypočítáte výstup sítě, když jsou známy vstup a váhy. Proces výpočtu výstupu neuronové sítě daný těmito hodnotami se nazývá dopředný průchod neboli proces.
3 Průchod vpřed
Abychom demonstrovali, jak vypočítat výstup ze vstupu v neuronových sítích, začněme konkrétním případem třívrstvé neuronové sítě, který byl uveden výše. Níže je uveden ve formě rovnice, poté bude demonstrován na konkrétním příkladu a nějakém kódu Pythonu:
$$ \begin{align} h_1^{(2)} &= f(w_{11}^{(1)}x_1 + w_{12}^{(1)} x_2 + w_{13}^{(1)} x_3 + b_1^{(1)}) \\ h_2^{(2)} &= f(w_{21}^{(1)}x_1 + w_{22}^{(1)} x_2 + w_{23}^{(1)} x_3 + b_2^{(1)}) \\ h_3^{(2)} &= f(w_{31}^{(1)}x_1 + w_{32}^{(1)} x_2 + w_{33}^{(1)} x_3 + b_3^{(1)}) \\ h_{W,b}(x) &= h_1^{(3)} = f(w_{11}^{(2)}h_1^{(2)} + w_{12}^{(2)} h_2^{(2)} + w_{13}^{(2)} h_3^{(2)} + b_1^{(2)}) \end{align} $$
Ve výše uvedené rovnici $f(bullet)$ odkazuje na funkci aktivace uzlu, v tomto případě na sigmoidní funkci. První řádek, ${h_1}^{(2)}$ je výstupem prvního uzlu ve druhé vrstvě a jeho vstupy jsou $w_{11}^{(1)}x_1$, $w_{12} ^{(1)} x_2$, $w_{13}^{(1)}x_3$ a $b_1^{(1)}$. Tyto vstupy lze vysledovat ve výše uvedeném třívrstvém schématu zapojení. Jednoduše se sečtou a poté projdou aktivační funkcí pro výpočet výstupu prvního uzlu. Stejně tak pro další dva uzly ve druhé vrstvě.
Poslední linka je výstupem jediného uzlu ve třetí a poslední vrstvě, což je konečný výstup neuronové sítě. Jak lze pozorovat, místo převzetí vážených vstupních proměnných ($x_1, x_2, x_3$) konečný uzel bere jako vstup vážený výstup uzlů druhé vrstvy ($h_{1}^{(2)} $, $h_{2}^{(2)}$, $h_{3}^{(2)}$), plus vážené zkreslení. Ve formě rovnic tedy můžete vidět hierarchickou povahu umělých neuronových sítí.
3.1 Dopředný příklad
Nyní si udělejme jednoduchý první příklad výstupu této neuronové sítě v Pythonu. Nejprve si všimněte, že váhy mezi vrstvou 1 a 2 ($w_{11}^{(1)}, w_{12}^{(1)}, dots$) jsou ideální pro reprezentaci matic? Pozorovat:
$$ \begin{equation} W^{(1)} = \begin{pmatrix} w_{11}^{(1)} & w_{12}^{(1)} & w_{13}^{(1)} \\ w_{21}^{(1)} & w_{22}^{(1)} & w_{23}^{(1)} \\ w_{31}^{(1)} & w_{32}^{(1)} & w_{33}^{(1)} \\ \end{pmatrix} \end{equation} $$
Tuto matici lze snadno reprezentovat pomocí numpy polí:
[pastacode lang=”python” manual=”import%20numpy%20as%20np%0Aw1%20%3D%20np.array(%5B%5B0.2%2C%200.2%2C%200.2%5D%2C%20%5B0 .4%2C%200.4%2C%200.4%5D%2C%20%5B0.6%2C%200.6%2C%200.6%5D%5D)” message=”” highlight=”” provider=”manual”/]
Zde jsem právě naplnil pole závaží vrstvy 1 několika příkladnými závažími. Totéž můžeme udělat pro pole vah vrstvy 2:
$$ \begin{equation} W^{(1)} = \begin{pmatrix} w_{11}^{(1)} & w_{12}^{(1)} & w_{13}^{(1)} \\ w_{21}^{(1)} & w_{22}^{(1)} & w_{23}^{(1)} \\ w_{31}^{(1)} & w_{32}^{(1)} & w_{33}^{(1)} \\ \end{pmatrix} \end{equation} $$
w2 = np.zeros((1, 3))
w2[0,:] = np.array([0. 5, 0.5, 0.5])Můžeme také nastavit některé fiktivní hodnoty v poli/vektoru váhy zkreslení vrstvy 1 a váhy zkreslení vrstvy 2 (což je pouze jediná hodnota v této struktuře neuronové sítě – tj. skalár):
b1 = np.array([0.8, 0.8, 0.8])
b2 = np.array([0.2 ])Nakonec, než napíšeme hlavní program pro výpočet výstupu z neuronové sítě, je užitečné nastavit samostatnou funkci Pythonu pro aktivační funkci:
def f(x):
return 1 / (1 + np.exp(-x) )3.2 Náš první pokus o dopřednou funkci
Níže je uveden jednoduchý způsob výpočtu výstupu neuronové sítě pomocí vnořených smyček v pythonu. Brzy se podíváme na efektivnější způsoby výpočtu výstupu.
def simple_looped_nn_calc(n_layers, x, w, b):
for l in range(n_layers-1):
#Setup the input array which the weights will be multiplied by for each layer
#If it’s the first layer, the input array will be the x input vector
#If it’s not the first layer, the input to the next layer will be the
#output of the previous layer
if l == 0:
node_in = x
else:
node_in = h
#Setup the output array for the nodes in layer l + 1
h = np.zeros((w[l].shape[0],))
#loop through the rows of the weight array
for i in range(w[l].shape[0]):
#setup the sum inside the activation function
f_sum = 0
#loop through the columns of the weight array
for j in range(w[l].shape[1]):
f_sum += w[l][i][j] * node_in[j]
#add the bias
f_sum += b[l][i]
#finally use the activation function to calculate the
#i-th output i.e. h1, h2, h3
h[i] = f(f_sum)
return hTato funkce bere jako vstup počet vrstev v neuronové síti, vstupní pole/vektor x, pak pythonovské n-tice nebo seznamy vah a váhových zkreslení sítě, přičemž každý prvek v n-tice/seznamu představuje vrstvu $l$ v síti. Jinými slovy, vstupy jsou nastaveny následovně:
w = [w1, w2]
b = [b1, b2]
#a dummy x input vector
x = [1.5, 2.0, 3.0]Funkce nejprve zkontroluje, jaký je vstup do vrstvy uvažovaných uzlů/váh. Pokud se díváme na první vrstvu, vstupem do uzlů druhé vrstvy je vstupní vektor $x$ vynásobený příslušnými váhami. Po první vrstvě jsou však vstupy do následujících vrstev výstupem předchozích vrstev. Nakonec existuje vnořená smyčka přes příslušné hodnoty $i$ a $j$ váhových vektorů a vychýlení. Funkce používá rozměry vah pro každou vrstvu, aby zjistila počet uzlů a tedy strukturu sítě.
Volání funkce:
simple_looped_nn_calc(3, x, w, b)dává výstup 0,8354. Tyto výsledky můžeme potvrdit ručním provedením výpočtů v původních rovnicích:
$$ \begin{align} h_1^{(2)} &= f(0.2*1.5 + 0.2*2.0 + 0.2*3.0 + 0.8) = 0.8909 \\ h_2^{(2)} &= f(0.4*1.5 + 0.4*2.0 + 0.4*3.0 + 0.8) = 0.9677 \\ h_3^{(2)} &= f(0.6*1.5 + 0.6*2.0 + 0.6*3.0 + 0.8) = 0.9909 \\ h_{W,b}(x) &= h_1^{(3)} = f(0.5*0.8909 + 0.5*0.9677 + 0.5*0.9909 + 0.2) = 0.8354 \end{align} $$
3.3 Efektivnější provádění
Jak již bylo řečeno dříve – použití smyček není nejúčinnějším způsobem výpočtu kroku vpřed v Pythonu. Je to proto, že cykly v Pythonu jsou notoricky pomalé. Brzy bude diskutován alternativní, efektivnější mechanismus provádění kroku vpřed v Pythonu a numpy. Můžeme porovnat, jak efektivní je algoritmus, pomocí funkce %timeit v IPythonu, která spustí funkci několikrát a vrátí průměrnou dobu, kterou funkce trvá:
[pastacode lang=”python” manual=”%25timeit%20simple_looped_nn_calc(3%2C%20x%2C%20w%2C%20b)” message=”” highlight=”” provider=”manual”/]
Spuštění tohoto nám říká, že smyčkový feed vpřed trvá $ 40 mil. s$. Výsledek v řádu desítek mikrosekund zní velmi rychle, ale při aplikaci na velmi velké praktické NN se stovkami uzlů na vrstvu se tato rychlost stane nepřístupnou, zejména při trénování sítě, jak bude zřejmé později v tomto tutoriálu. Pokud zkusíme čtyřvrstvou neuronovou síť pomocí stejného kódu, dostaneme výrazně horší výkon – ve skutečnosti 70 milionů $.
3.4 Vektorizace v neuronových sítích
Existuje způsob, jak napsat rovnice ještě kompaktněji a jak efektivněji vypočítat dopředný proces v neuronových sítích z výpočetní perspektivy. Za prvé, můžeme zavést novou proměnnou $z_{i}^{(l)}$, která je sčítaným vstupem do uzlu $i$ vrstvy $l$, včetně členu zkreslení. Takže v případě prvního uzlu ve vrstvě 2 se $z$ rovná:
$$ z_{1}^{(2)} = w_{11}^{(1)}x_1 + w_{12}^{(1)} x_2 + w_{13}^{(1)} x_3 + b_1^{(1)} = \sum_{j=1}^{n} w_{ij}^{(1)}x_i + b_{i}^{(1)} $$
kde n je počet uzlů ve vrstvě 1. Pomocí této notace lze nepraktickou předchozí sadu rovnic pro příklad třívrstvé sítě zredukovat na:
$$ \begin{align} z^{(2)} &= W^{(1)} x + b^{(1)} \\ h^{(2)} &= f(z^{(2)}) \\ z^{(3)} &= W^{(2)} h^{(2)} + b^{(2)} \\ h_{W,b}(x) &= h^{(3)} = f(z^{(3)}) \end{align} $$
Všimněte si použití velkého W k označení maticového tvaru vah. Je třeba poznamenat, že všechny prvky ve výše uvedené rovnici jsou nyní matice / vektory. Pokud tyto pojmy neznáte, budou podrobněji vysvětleny v další části. Lze výše uvedenou rovnici ještě více zjednodušit? Ano, může. Můžeme propagovat výpočty přes libovolný počet vrstev v neuronové síti zobecněním:
$$ \begin{align} z^{(l+1)} &= W^{(l)} h^{(l)} + b^{(l)} \\ h^{(l+1)} &= f(z^{(l+1)}) \end{align} $$
Zde můžeme vidět obecný dopředný proces, kde se výstup vrstvy $l$ stává vstupem do vrstvy $l+1$. Víme, že $h^{(1)}$ je jednoduše vstupní vrstva $x$ a $h^{(n_l)}$ (kde $n_l$ je počet vrstev v síti) je výstupem výstupu vrstva. Všimněte si ve výše uvedených rovnicích, že jsme vypustili odkazy na čísla uzlů $i$ a $j$ – jak to můžeme udělat? Nemusíme stále procházet a počítat všechny různé vstupy a výstupy uzlů?
Odpověď je, že k tomu můžeme použít násobení matic, abychom to udělali jednodušeji. Tento proces se nazývá „vektorizace“ a má dvě výhody – zaprvé zjednodušuje kód, jak brzy uvidíte. Zadruhé, můžeme v Pythonu (a dalších jazycích) používat rychlé rutiny lineární algebry spíše než používat smyčky, což urychlí naše programy. Numpy tyto výpočty snadno zvládne. Za prvé, pro ty, kteří nejsou obeznámeni s maticovými operacemi, je další část stručnou rekapitulací.
3.5 Maticové násobení
Rozšiřme $z^{(l+1)} = W^{(l)} h^{(l)} + b^{(l)}$ ve formě explicitní matice/vektoru pro vstupní vrstvu (tj. $ h^{(l)} = x$):
$$ \begin{align} z^{(2)} &= \begin{pmatrix} w_{11}^{(1)} & w_{12}^{(1)} & w_{13}^{(1)} \\ w_{21}^{(1)} & w_{22}^{(1)} & w_{23}^{(1)} \\ w_{31}^{(1)} & w_{32}^{(1)} & w_{33}^{(1)} \\ \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{pmatrix} + \begin{pmatrix} b_{1}^{(1)} \\ b_{2}^{(1)} \\ b_{3}^{(1)} \\ \end{pmatrix} \\ &= \begin{pmatrix} w_{11}^{(1)}x_{1} + w_{12}^{(1)}x_{2} + w_{13}^{(1)}x_{3} \\ w_{21}^{(1)}x_{1} + w_{22}^{(1)}x_{2} + w_{23}^{(1)}x_{3} \\ w_{31}^{(1)}x_{1} + w_{32}^{(1)}x_{2} + w_{33}^{(1)}x_{3} \\ \end{pmatrix} + \begin{pmatrix} b_{1}^{(1)} \\ b_{2}^{(1)} \\ b_{3}^{(1)} \\ \end{pmatrix} \\ &= \begin{pmatrix} w_{11}^{(1)}x_{1} + w_{12}^{(1)}x_{2} + w_{13}^{(1)}x_{3} + b_{1}^{(1)} \\ w_{21}^{(1)}x_{1} + w_{22}^{(1)}x_{2} + w_{23}^{(1)}x_{3} + b_{2}^{(1)} \\ w_{31}^{(1)}x_{1} + w_{32}^{(1)}x_{2} + w_{33}^{(1)}x_{3} + b_{3}^{(1)} \\ \end{pmatrix} \\ \end{align} $$
Pro ty, kteří si nejsou vědomi toho, jak maticové násobení funguje, je dobrý nápad prostudovat si maticové operace. Existuje mnoho stránek, které to dobře pokrývají. Nicméně, jen rychle, když je matice váhy vynásobena vektorem vstupní vrstvy, každý prvek v $řádku$ matice váh je vynásoben každým prvkem v jediném $sloupci$ vstupního vektoru a poté sečten a vytvoří se nový (3 x 1) vektor. Poté můžete jednoduše přidat vektor vah zkreslení, abyste dosáhli konečného výsledku.
Můžete pozorovat, jak každý řádek konečného výsledku výše odpovídá argumentu aktivační funkce v původní nematicové sadě rovnic výše. Pokud lze aktivační funkci aplikovat po prvcích (tj. na každý řádek zvlášť ve vektoru $z^{(1)}$), pak můžeme všechny naše výpočty provádět spíše pomocí matic a vektorů než pomocí pomalých smyček Pythonu. Naštěstí nám to numpy umožňuje s přiměřeně rychlými maticovými operacemi a funkcemi po prvcích. Pojďme se podívat na mnohem jednodušší (a rychlejší) verzi simple_looped_nn_calc:
def matrix_feed_forward_calc(n_layers, x, w, b):
for l in range(n_layers-1):
if l == 0:
node_in = x
else:
node_in = h
z = w[l].dot(node_in) + b[l]
h = f(z)
return hVšimněte si řádku 7, kde dochází k násobení matice – pokud při násobení vah vstupním vektorem uzlu v numpy použijete pouze symbol $*$, pokusí se provést nějaký druh násobení po prvcích, spíše než skutečné násobení matice, které jsme touha. Proto musíte při provádění násobení matic v numpy použít notaci a.dot(b) .
Pokud znovu provedeme %timeit pomocí této nové funkce a jednoduché 4vrstvé sítě, získáme pouze zlepšení o 24 mil. s$ (snížení ze 70 mil. s$ na 46 mil. s$). Pokud však zvětšíme velikost 4vrstvé sítě na vrstvy 100-100-50-10 uzlů, výsledky jsou mnohem působivější. Metoda založená na smyčkách v Pythonu zabere neuvěřitelných 41 milisekund $ – všimněte si, to jsou milisekundy, a vektorizovaná implementace trvá pouze 84 mil. s$, aby se vpřed množila neuronovou sítí. Použitím vektorizovaných výpočtů namísto smyček Pythonu jsme zvýšili efektivitu výpočtu 500krát! To je obrovské zlepšení. Existuje dokonce možnost rychlejší implementace maticových operací pomocí balíčků hlubokého učení, jako jsou TensorFlow a Theano, které využívají GPU vašeho počítače (spíše než CPU), jejichž architektura je vhodnější pro rychlé maticové výpočty (mám také výukový příspěvek TensorFlow).
Tím se dostáváme ke konci dopředného úvodu pro neuronové sítě. Další část se bude zabývat tím, jak vlastně trénovat neuronovou síť tak, aby mohla provádět klasifikační úkoly pomocí gradientního sestupu a zpětného šíření.