17.12.2022 Machine Learning #tensorflow #machine #learning

Tento tutoriál o konvolučních neuronových sítích představí tyto sítě tím, že je vytvoří v TensorFlow .

Vícevrstvé neuronové sítě mohou docela dobře předpovídat věci, jako jsou číslice v datové sadě MNIST. To platí zejména tehdy, použijeme-li některá vylepšení. Proč tedy potřebujeme jinou architekturu? Za prvé – datová sada MNIST je docela jednoduchá. Obrázky jsou malé (pouze 28 x 28 pixelů), jsou jednovrstvé (tj. ve stupních šedi, spíše než barevný 3vrstvý RGB obrázek) a obsahují docela jednoduché tvary (pouze číslice, žádné jiné objekty). Jakmile se začneme snažit klasifikovat věci do složitějších barevných obrázků, jako jsou autobusy, auta, vlaky atd., narazíme na problémy s přesností. Co uděláme?

Nejprve se můžeme pokusit zvýšit počet vrstev v naší neuronové síti, aby byla hlubší. To zvýší složitost sítě a umožní nám modelovat složitější funkce. Bude to však něco stát – počet parametrů (tj. hmotností a vychýlení) se rapidně zvýší. Díky tomu je model náchylnější k přeučení a prodlouží dobu tréninku. Ve skutečnosti se učení tak obtížných problémů může stát neřešitelným pro normální neuronové sítě. To nás vede k řešení – konvoluční neuronové sítě.

Co je to konvoluční neuronová síť?

Nejčastěji spojovanou myšlenkou s konvolučními neuronovými sítěmi je myšlenka „pohybujícího se filtru“ , který prochází obrazem. Tento pohyblivý filtr nebo konvoluce se vztahuje na určité okolí uzlů (což mohou být vstupní uzly, tj. pixely), jak je znázorněno níže, kde použitý filtr je 0,5 x hodnota uzlu:

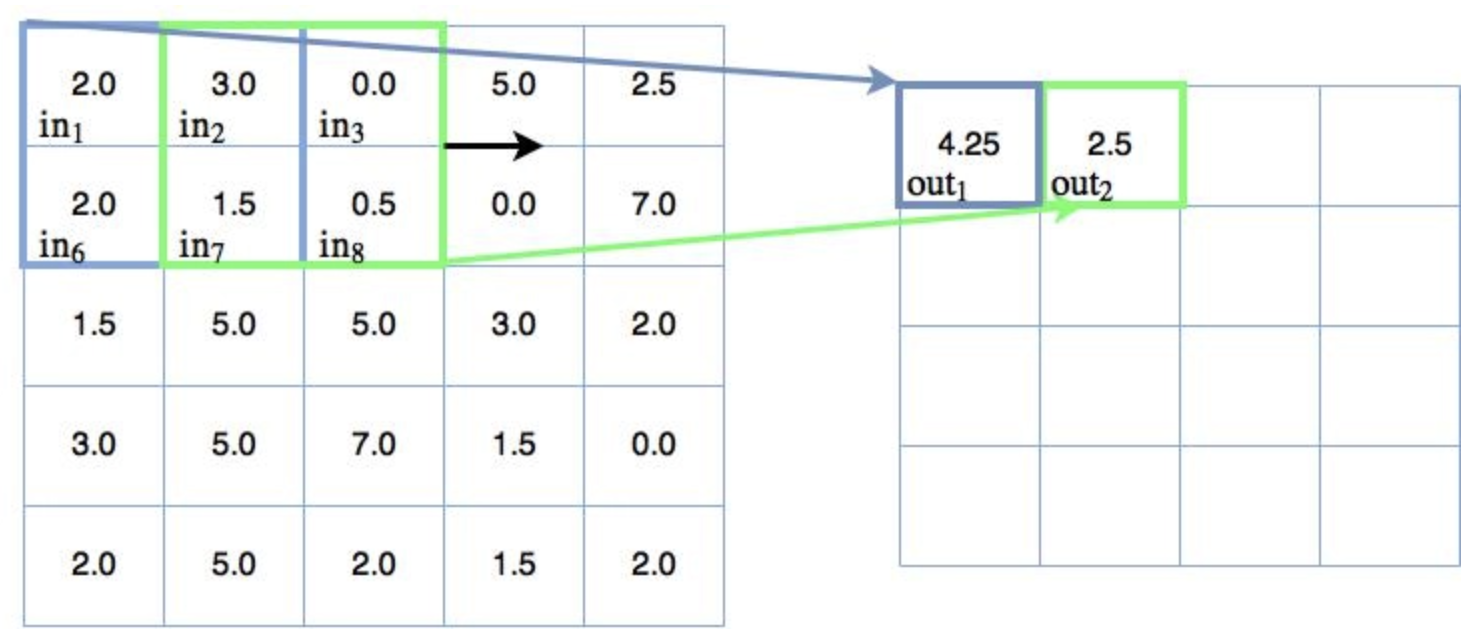
Pohyblivý filtr 2×2 (všechny váhy = 0,5)

Jak lze pozorovat, byly ukázány pouze dva výstupy pohyblivého/konvolučního filtru – zde mapujeme vstupní čtverec 2×2 do jediného výstupního uzlu. Váha mapování každého vstupního čtverce, jak již bylo zmíněno, je 0,5 napříč všemi čtyřmi vstupy. Jinými slovy, byly provedeny následující výpočty:

$$ \begin{align} out_1 &= 0.5 in_1 + 0.5 in_2 + 0.5 in_6 + 0.5 in_7 \\ &= 0.5 \times 2.0 + 0.5 \times 3.0 + 0.5 \times 2.0 + 0.5 \times 1.5 \\ &= 4.25 \\ out_2 &= 0.5 in_2 + 0.5 in_3 + 0.5 in_7 + 0.5 in_8 \\ &= 0.5 \times 3.0 + 0.5 \times 0.0 + 0.5 \times 1.5 + 0.5 \times 0.5 \\ &= 2.5 \\ \end{align} $$

Při operaci konvoluce by se tento pohyblivý filtr 2×2 míchal napříč každou možnou kombinací souřadnic x a y , aby naplnil výstupní uzly. Tuto operaci lze také ilustrovat pomocí našich standardních diagramů uzlů neuronové sítě:

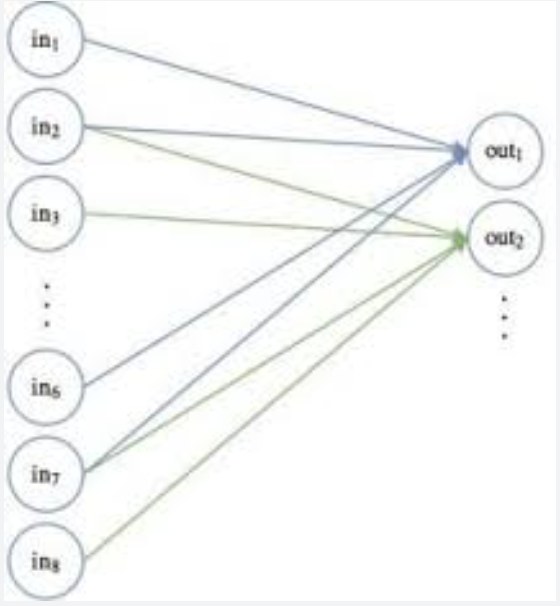
Pohyblivý filtr 2×2 – diagram uzlů

První poloha připojení pohyblivého filtru je znázorněna modrými čarami, druhá (x + 1) je znázorněna zelenými čarami. Váhy těchto spojení jsou v tomto příkladu všechny rovny 0,5.

Na této konvoluční operaci lze ve srovnání s naším předchozím chápáním standardních neuronových sítí pozorovat několik věcí :

Řídká spojení – všimněte si, že ne každý vstupní uzel je připojen k výstupním. To je v rozporu s plně propojenými neuronovými sítěmi, kde je každý uzel v jedné vrstvě spojen s každým uzlem v následující vrstvě.
Konstantní parametry filtru / váhy – každý filtr má konstantní parametry. Jinými slovy, jak se filtr pohybuje po obrázku, jsou aplikovány stejné váhy. Každý filtr tedy provede určitou transformaci napříč celým obrazem. To je na rozdíl od plně propojených neuronových sítí, které mají pro každé připojení jinou hodnotu váhy
- Všimněte si, neříkám, že každá váha je ve filtru konstantní, jako v příkladu výše (tj. s vahami [0,5, 0,5, 0,5, 0,5]). Váhy ve filtru mohou být libovolnou kombinací hodnot v závislosti na tom, jak jsou filtry trénovány.

Tyto dvě vlastnosti konvolučních neuronových sítí mohou výrazně snížit počet parametrů požadovaných v síti ve srovnání s plně propojenými neuronovými sítěmi.

Výstup konvolučního mapování pak prochází nějakou formou nelineární aktivační funkce, často aktivační funkcí rektifikované lineární jednotky.

Tento krok v konvolučních neuronových sítích se často nazývá mapování vlastností. Než přejdeme k dalšímu hlavnímu rysu konvolučních neuronových sítí, sdružování , stojí za to říci pár věcí o této myšlence.

Mapování funkcí a více kanálů

Již dříve jsem zmínil, že parametry filtru, tj. váhy, jsou udržovány konstantní, když se filtr pohybuje přes vstup. To umožňuje, aby byl filtr trénován, aby rozpoznával určité funkce ve vstupních datech. V případě obrázků se může naučit rozpoznávat tvary, jako jsou linie, hrany a další výrazné tvary. To je důvod, proč se konvoluční krok často nazývá mapování prvků . Abychom však mohli dobře klasifikovat, v každé konvoluční fázi obvykle potřebujeme více filtrů. Ve skutečnosti tedy výše uvedený diagram pohyblivého filtru vypadá takto:

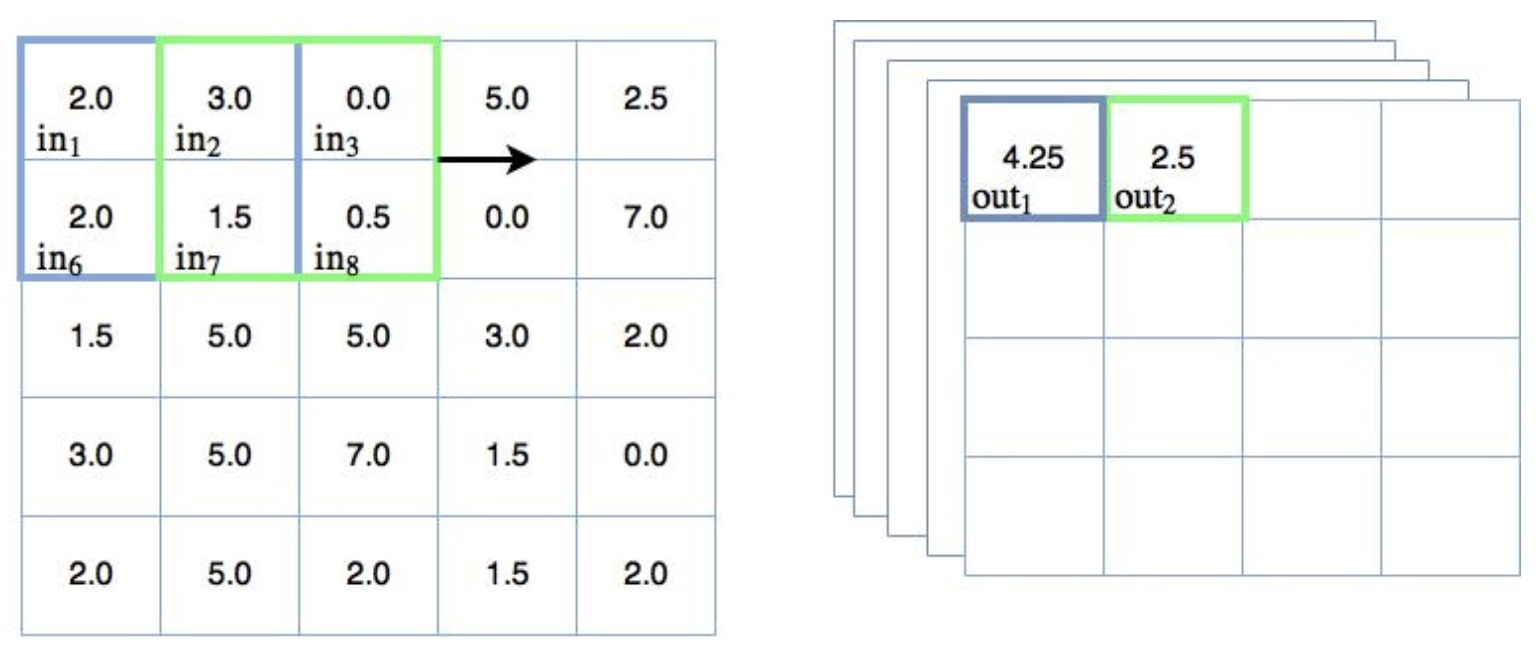
Více konvolučních filtrů

Vpravo nyní můžete vidět naskládané výstupy a to, že každý samostatně trénovaný filtr vytváří svůj vlastní 2D výstup (pro 2D obraz). Toto je často odkazoval se na jak mít více kanálů . Každý z těchto kanálů bude trénován tak, aby detekoval určité klíčové prvky v obraze. Výstup konvoluční vrstvy tedy bude ve skutečnosti 3rozměrný (opět pro 2D obraz). Pokud je samotný vstup vícekanálový, jako v případě barevného obrazu s vrstvami RGB, výstup konvoluční vrstvy bude 4D . Naštěstí, jak bude ukázáno později, TensorFlow zvládne všechna tato mapování docela snadno.

Nezapomeňte, že konvoluční výstup pro každý uzel přes všechny kanály prochází aktivační funkcí.

Další důležitá část konvolučních neuronových sítí se nazývá sdružování.

Sdružování

Myšlenka sdružování v konvolučních neuronových sítích spočívá ve dvou věcech:

Snižte počet parametrů ve vaší síti (sdružování se z tohoto důvodu také nazývá „down-sampling“).
Aby byla detekce prvků robustnější tím, že bude odolnější vůči změnám měřítka a orientace

Co je tedy sdružování? Opět se jedná o techniku typu „posuvné okno“, ale v tomto případě namísto použití vah sdružování aplikuje na hodnoty v okně nějakou statistickou funkci. Nejčastěji se používá funkce max(), takže maximální sdružování bude mít maximální hodnotu v okně. Někdy se také používají jiné varianty, jako je střední sdružování nebo sdružování podle normy L2. V tomto tutoriálu pro konvoluční neuronové sítě se však zaměříme pouze na maximální sdružování. Níže uvedený diagram ukazuje některé maximální sdružování v akci:

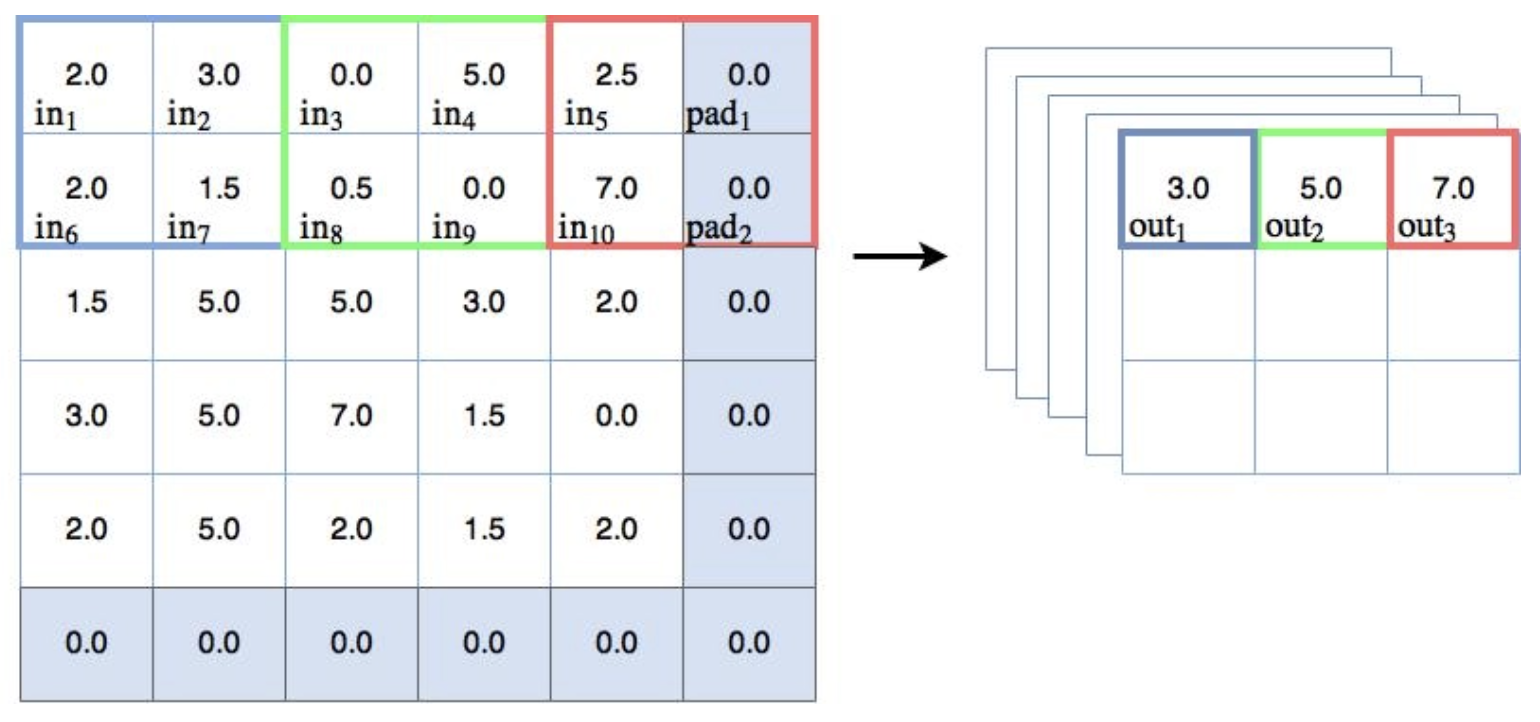
Příklad maximálního sdružování (s odsazením)

Projdeme si několik bodů souvisejících s výše uvedeným diagramem:

Základní funkce

Jak je vidět na výše uvedeném diagramu, různobarevná políčka na vstupních uzlech/čtvercích představují posuvné okno 2×2. Max sdružování se provádí na uzlech v posuvném okně, tj. z výstupu uzlů se bere prosté maximum. Jinými slovy:

$$ \begin{align} out_1 &= max(in_1, in_2, in_6, in_7) \\ out_2 &= max(in_3, in_4, in_8, in_9) \\ out_3 &= max(in_5, pad_1, in_{10}, pad_2) \\ \end{align} $$

Kroky a sestupné vzorkování

Možná jste si všimli, že ve výše uvedeném příkladu konvolučního / pohyblivého filtru se filtr 2×2 posunul pouze o jedno místo ve směru x a y skrz obraz / vstup. To vedlo k překrývání filtračních oblastí. Toto se nazývá krok [1, 1] – to znamená, že se filtr posune o 1 krok ve směru x a y . Při maximálním sdružování je krok obvykle nastaven tak, aby se regiony nepřekrývaly. V tomto případě potřebujeme krok 2 (nebo [2, 2]), abychom se vyhnuli překrývání. To lze pozorovat na obrázku výše, když se maximální sdružovací box posune o dva kroky v xsměr. Všimněte si, že krok 2 ve skutečnosti snižuje rozměrnost výstupu. Přešli jsme od vstupní mřížky 5×5 (prozatím ignorujeme výplň 0,0) k výstupní mřížce 3×3 – nazývá se to down-sampling a lze ji použít ke snížení počtu parametrů v modelu.

Vycpávka

Na obrázku výše si všimnete šedých stínovaných rámečků kolem vnější strany, všechny s 0,0 uprostřed. Jedná se o vycpávkové uzly – falešné uzly, které jsou zavedeny tak, aby 2×2 max. sdružovací filtr mohl provést 3 kroky ve směrech x a y s krokem 2, přestože existuje pouze 5 uzlů k procházení buď ve směru x nebo y . Vzhledem k tomu, že hodnoty jsou 0,0, s opravenou aktivací lineární jednotky předchozí vrstvy (která nemůže mít na výstupu záporné číslo), nebudou tyto uzly ve skutečnosti nikdy vybrány v procesu maximálního sdružování. TensorFlow má možnosti výplně, které je třeba vzít v úvahu, a ty budou diskutovány později v tutoriálu.

To popisuje, jak funguje sdružování, ale proč je součástí konvolučních neuronových sítí?

Proč se v konvolučních neuronových sítích používá sdružování?

Kromě funkce down-samplingu se v konvolučních neuronových sítích používá sdružování, aby byla detekce určitých prvků ve vstupu invariantní vůči změnám měřítka a orientace. Jiný způsob uvažování o tom, co dělají, je, že zobecňují na nižší úrovni, složitější informace. Vezměme si případ, kdy máme řadu konvolučních filtrů, které se během tréninku naučily detekovat číslici „9“ v různých orientacích ve vstupních obrázcích. Aby se konvoluční neuronová síť naučila správně klasifikovat vzhled „9“ na obrázku, musí se nějakým způsobem aktivovat bez ohledu na to, jaká je orientace číslice (kromě případů, kdy vypadá jako „6“, tj. ). S tím může sdružování pomoci, zvažte následující schéma:

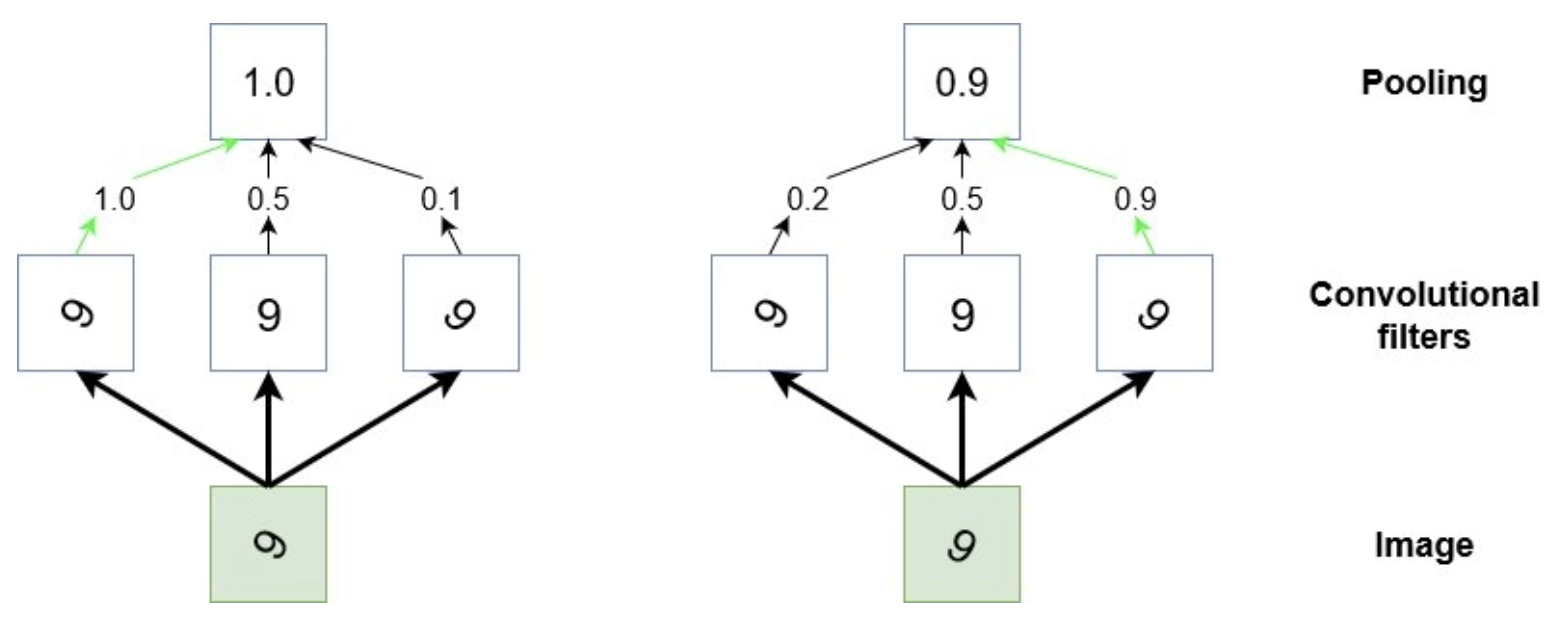
Stylizované znázornění sdružování

Výše uvedený diagram je jakousi stylizovanou reprezentací operace sdružování. Uvažujme malou oblast vstupního obrázku, která má v sobě číslici „9“ (zelené pole). Během tréninku máme několik konvolučních filtrů, které se naučily aktivovat, když na obrázku „vidí“ tvar „9“, ale aktivují se nejsilněji v závislosti na orientaci této „9“. Chceme, aby konvoluční neuronová síť rozpoznala „9“ bez ohledu na to, v jaké je orientaci. Sdružování tedy „prohlíží“ výstup těchto tří filtrů a bude poskytovat vysoký výkon, pokud má kterýkoli z těchto filtrů vysokou aktivace.

Sdružování funguje jako zobecnění informací nižší úrovně a umožňuje nám tak přejít od dat s vysokým rozlišením k informacím s nižším rozlišením . Jinými slovy, sdružování ve spojení s konvolučními filtry se pokouší detekovat objekty v obraze.

Konečný obrázek

Níže uvedený obrázek z Wikipedie ukazuje konečný obrázek plně vyvinuté konvoluční neuronové sítě:

Plně konvoluční neuronová síť – od Aphex34 (vlastní práce) [ CC BY-SA 4.0 ], prostřednictvím Wikimedia Commons

Pojďme si projít tento obrázek zleva doprava. Nejprve máme vstupní obrázek robota. Poté několik konvolučních filtrů (tyto by zahrnovaly aktivaci rektifikované lineární jednotky), následované sdružováním / dílčím vzorkováním. Pak máme další vrstvu konvoluce a sdružování. Všimněte si počtu kanálů (naskládaných modrých čtverců) a zmenšení velikostí x, y každého kanálu, protože ve sdružených vrstvách dochází k dílčímu vzorkování / podvzorkování. Konečně se dostáváme k plně propojené vrstvě před výstupem. Tato vrstva ještě nebyla zmíněna a zaslouží si diskusi.

Plně propojená vrstva

Na výstupu vrstev konvolučního sdružování jsme se posunuli od dat s vysokým rozlišením a nízkou úrovní o pixelech k reprezentacím objektů v obraze. Účelem těchto finálních, plně propojených vrstev je provést klasifikaci těchto objektů – jinými slovy, na konec trénovaného detektoru objektů přišroubujeme standardní klasifikátor neuronové sítě. Jak můžete pozorovat, výstupem konečné sdružovací vrstvy je mnoho kanálů matic x x y. Abychom spojili výstup sdružovací vrstvy s plně propojenou vrstvou, musíme tento výstup zploštit do jediného (N x 1) tenzoru.

Řekněme, že máme 100 kanálů 2 x 2 sdružovacích matic. To znamená, že musíme všechna tato data sloučit do vektoru s jedním sloupcem a 2 x 2 x 100 = 400 řádky. Níže ukážu, jak to můžeme udělat v TensorFlow.

Nyní jsme probrali základy toho, jak jsou konvoluční neuronové sítě strukturovány a proč jsou takto vytvořeny. Nyní je čas ukázat, jak takovou síť implementujeme v TensorFlow.

Konvoluční neuronová síť založená na TensorFlow

TensorFlow usnadňuje vytváření konvolučních neuronových sítí, jakmile pochopíte některé nuance rámce, jak s nimi zacházet. V tomto tutoriálu vytvoříme konvoluční neuronovou síť se strukturou podrobně popsanou na obrázku níže. Síť, kterou se chystáme vybudovat, bude provádět klasifikaci číslic MNIST.

Příklad konvoluční neuronové sítě

Jak lze pozorovat, začínáme s obrázky číslic ve stupních šedi MNIST 28×28. Poté vytvoříme 32, 5×5 konvolučních filtrů / kanálů plus aktivace uzlů ReLU (rektifikovaná lineární jednotka). Poté máme stále výšku a šířku 28 uzlů. Poté provedeme down-sampling použitím operace 2×2 max pooling s krokem 2. Vrstva 2 se skládá ze stejné struktury, ale nyní s 64 filtry / kanály a dalším krokem-2 max pooling down-sample. Poté výstup zploštíme, abychom získali plně propojenou vrstvu s 3164 uzly, následovanou další skrytou vrstvou 1000 uzlů. Tyto vrstvy budou používat aktivace uzlů ReLU. Nakonec použijeme klasifikační vrstvu softmax pro výstup 10místné pravděpodobnosti.

Pojďme si projít kód.

Vstupní data a zástupné symboly

Níže uvedený kód nastavuje vstupní data a zástupné symboly pro klasifikátor.

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

# Python optimisation variables
learning_rate = 0.0001
epochs = 10
batch_size = 50

# declare the training data placeholders
# input x - for 28 x 28 pixels = 784 - this is the flattened image data that is drawn from 
# mnist.train.nextbatch()
x = tf.placeholder(tf.float32, [None, 784])
# dynamically reshape the input
x_shaped = tf.reshape(x, [-1, 28, 28, 1])
# now declare the output data placeholder - 10 digits
y = tf.placeholder(tf.float32, [None, 10])

TensorFlow má praktický zavaděč pro data MNIST, která jsou seřazeny v prvních několika řádcích. Poté máme několik deklarací proměnných, které určují chování optimalizace (rychlost učení, velikost dávky atd.). Dále deklarujeme zástupný symbol pro vstupní obrazová data, x. Vstupní data obrazu budou extrahována pomocí funkce mnist.train.nextbatch(), která poskytuje zploštělý uzel 28×28=784, jednokanálovou reprezentaci obrazu ve stupních šedi. Než však budeme moci tato data použít v konvolučních a sdružovacích funkcích TensorFlow, jako je conv2d() a max_pool(), musíme data přetvořit, protože tyto funkce berou pouze 4D data.

Formát dodávaných dat je [i, j, k, l], kde i je počet tréninkových vzorků, j je výška obrazu, k je váha a l je číslo kanálu. Protože máme obrázek ve stupních šedi, bude l vždy rovno 1 (pokud bychom měli RGB obrázek, bylo by to rovno 3). Obrázky MNIST jsou 28 x 28, takže j a k se rovnají 28. Když přetváříme vstupní data x na x_shaped, teoreticky neznáme velikost prvního rozměru x, takže nevíme, co já jsem. Nicméně tf.reshape() nám umožňuje vložit -1 místoi a bude se dynamicky přetvářet na základě počtu trénovacích vzorků, jak se trénování provádí. Takže použijeme [-1, 28, 28, 1] pro druhý argument v tf.reshape().

Nakonec potřebujeme zástupný symbol pro naše výstupní trénovací data, což je tenzor velikosti [?, 10] – kde 10 znamená 10 možných klasifikovaných číslic. Použijeme mnist.train.next_batch() k extrahování štítků číslic jako jeden aktuální vektor – jinými slovy, číslice „3“ bude reprezentována jako [0, 0, 0, 1, 0, 0, 0, 0, 0, 0].

Definování vrstev konvoluce

Protože musíme vytvořit několik konvolučních vrstev, je nejlepší vytvořit funkci pro omezení opakování:

def create_new_conv_layer(input_data, num_input_channels, num_filters, filter_shape, pool_shape, name):
    # setup the filter input shape for tf.nn.conv_2d
    conv_filt_shape = [filter_shape[0], filter_shape[1], num_input_channels,
                      num_filters]

    # initialise weights and bias for the filter
    weights = tf.Variable(tf.truncated_normal(conv_filt_shape, stddev=0.03),
                                      name=name+’_W’)
    bias = tf.Variable(tf.truncated_normal([num_filters]), name=name+’_b’)

    # setup the convolutional layer operation
    out_layer = tf.nn.conv2d(input_data, weights, [1, 1, 1, 1], padding=’SAME’)

    # add the bias
    out_layer += bias

    # apply a ReLU non-linear activation
    out_layer = tf.nn.relu(out_layer)

    # now perform max pooling
    ksize = [1, pool_shape[0], pool_shape[1], 1]
    strides = [1, 2, 2, 1]
    out_layer = tf.nn.max_pool(out_layer, ksize=ksize, strides=strides, 
                               padding=’SAME’)

    return out_layer

Níže projdu každý řádek/blok této funkce:

conv_filt_shape = [filter_shape[0], filter_shape[1], num_input_channels,
                      num_filters]

Tento řádek nastavuje proměnnou pro udržení tvaru závaží, které určují chování konvolučního filtru 5×5. Formát, který funkce conv2d() pro filtr přijímá, je: [výška_filtru, šířka_filtru, in_channels, out_channels]. Výška a šířka filtru jsou uvedeny v proměnných filter_shape (v tomto případě [5, 5]). Počet vstupních kanálů pro první konvoluční vrstvu je jednoduše 1, což odpovídá jednokanálovému snímku ve stupních šedi MNIST. Pro druhou konvoluční vrstvu však bere výstup první konvoluční vrstvy, která má 32 kanálový výstup. Pro druhou konvoluční vrstvu je tedy vstupních kanálů 32. Jak je definováno v blokovém schématu výše, počet výstupních kanálů první vrstvy je 32 a pro druhou vrstvu je to 64.

# initialise weights and bias for the filter
weights = tf.Variable(tf.truncated_normal(conv_filt_shape, stddev=0.03),
                                  name=name+’_W’)
bias = tf.Variable(tf.truncated_normal([num_filters]), name=name+’_b’)

V těchto řádcích vytvoříme váhy a předpětí pro konvoluční filtr a náhodně inicializujeme tenzory.

# setup the convolutional layer operation
out_layer = tf.nn.conv2d(input_data, weights, [1, 1, 1, 1], padding=’SAME’)

Na tomto řádku nastavujeme provoz konvolučního filtru. Proměnná input_data je samozřejmá, stejně jako váhy. Velikost tenzoru závaží ukazuje TensorFlow, jakou velikost by měl mít konvoluční filtr. Další argument [1, 1, 1, 1] je parametr strides , který je vyžadován v conv2d(). V tomto případě chceme, aby se filtr pohyboval v krocích po 1 ve směru x a y (nebo ve směru na výšku a šířku). Tato informace je předávána v hodnotách kroků[1] a kroků[2] – obě jsou v tomto případě rovné 1. První a poslední hodnoty kroků jsou vždy rovny 1, pokud by nebyly, přesouvali bychom filtr mezi tréninkovými vzorky nebo mezi kanály, což nechceme dělat. Posledním parametrem je výplň. Výplň určuje výstupní velikost každého kanálu, a když je nastavena na „STEJNÉ“, vytváří rozměry:

out_height = ceil(float(in_height) / float(strides[1]))
out_width = ceil(float(in_width) / float(strides[2]))

Pro první konvoluční vrstvu platí, že in_height = in_width = 28 a strides[1] = strides[2] = 1 . Proto bude výplň vstupu 0,0 uzly uspořádána tak, že out_height = out_width = 28 – nedojde ke změně velikosti výstupu. Tato výplň má zabránit skutečnosti, že při procházení obrázku velikosti ( x, y) nebo vstupu s konvolučním filtrem velikosti ( n, m) by s krokem 1 byl výstup ( x-n+1,y -m+1) . Takže v tomto případě bez vyplnění by výstupní velikost byla (24,24). Chceme, aby velikosti výstupů byly snadno sledovatelné, proto jsme jako výplň zvolili možnost „STEJNÉ“, abychom zachovali stejnou velikost.

# add the bias
out_layer += bias
# apply a ReLU non-linear activation
out_layer = tf.nn.relu(out_layer)

Ve dvou výše uvedených řádcích jednoduše přidáme předpětí k výstupu konvolučního filtru a poté aplikujeme nelineární aktivační funkci ReLU.

# now perform max pooling
ksize = [1, pool_shape[0], pool_shape[1], 1]
strides = [1, 2, 2, 1]
out_layer = tf.nn.max_pool(out_layer, ksize=ksize, strides=strides, 
                               padding=’SAME’)

return out_layer

Funkce max_pool() bere tenzor jako svůj první vstup, přes který se provádí sdružování. Další dva argumenty ksize a kroky definují operaci sdružování. Ignorování první a poslední hodnoty těchto vektorů (které budou vždy nastaveny na 1), prostřední hodnoty ksize (pool_shape[0] a pool_shape[1]) definují tvar max poolingového okna ve směru x a y. V tomto příkladu konvolučních neuronových sítí používáme maximální velikost sdružovacího okna 2×2. Totéž platí pro vektor kroků – protože chceme vzorkovat dolů, v tomto příkladu vybíráme kroky o velikosti 2 v obou xay směry (strides[1] a strides [2]). Tím se vstupní velikost rozměrů ( x,y ) zmenší na polovinu.

Konečně máme další příklad argumentu výplně. Pro volbu 'SAME' platí stejná pravidla jako pro konvoluční funkci conv2d(). A to:

out_height = ceil(float(in_height) / float(strides[1]))
out_width = ceil(float(in_width) / float(strides[2]))

Vyražením hodnot 2 pro strides[1] a strides[2] pro první konvoluční vrstvu získáme výstupní velikost (14, 14). Toto je poloviční velikost vstupu (28, 28), což je to, co hledáme. TensorFlow opět uspořádá vycpávku tak, aby bylo dosaženo tohoto výstupního tvaru, což pro nás dělá věci pěkné a čisté.

Nakonec vrátíme objekt out_layer, který je vlastně samostatným podgrafem obsahujícím všechny operace a proměnné váhy v něm. Dvě konvoluční vrstvy vytvoříme v hlavním programu voláním následujících příkazů:

# create some convolutional layers
layer1 = create_new_conv_layer(x_shaped, 1, 32, [5, 5], [2, 2], name=’layer1′)
layer2 = create_new_conv_layer(layer1, 32, 64, [5, 5], [2, 2], name=’layer2′)

ak můžete vidět, vstup do vrstvy1 je tvarovaný vstup ve tvaru x a vstup do vrstvy2 je výstup první vrstvy. Nyní můžeme přejít k vytváření plně propojených vrstev.

Plně propojené vrstvy

Jak bylo diskutováno dříve, nejprve musíme vyrovnat výstup z konečné konvoluční vrstvy. Nyní je to mřížka 7×7 uzlů se 64 kanály, což odpovídá 3136 uzlům na tréninkový vzorek. Můžeme použít tf.reshape() k tomu, co potřebujeme:

flattened = tf.reshape(layer2, [-1, 7 * 7 * 64])

Opět máme dynamicky vypočítanou první dimenzi (-1 výše), odpovídající počtu vstupních vzorků v trénovací dávce. Dále nastavíme první plně připojenou vrstvu:

# setup some weights and bias values for this layer, then activate with ReLU
wd1 = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1000], stddev=0.03), name=’wd1′)
bd1 = tf.Variable(tf.truncated_normal([1000], stddev=0.01), name=’bd1′)
dense_layer1 = tf.matmul(flattened, wd1) + bd1
dense_layer1 = tf.nn.relu(dense_layer1)

V podstatě inicializujeme váhy plně připojené vrstvy, násobíme je zploštělým konvolučním výstupem a pak přidáváme předpětí. Nakonec se použije aktivace ReLU. Další vrstva je definována:

# another layer with softmax activations
wd2 = tf.Variable(tf.truncated_normal([1000, 10], stddev=0.03), name=’wd2′)
bd2 = tf.Variable(tf.truncated_normal([10], stddev=0.01), name=’bd2′)
dense_layer2 = tf.matmul(dense_layer1, wd2) + bd2
y_ = tf.nn.softmax(dense_layer2)

Tato vrstva se připojuje k výstupu, a proto používáme aktivaci soft-max k vytvoření predikovaných výstupních hodnot y_ . Nyní jsme definovali základní strukturu naší konvoluční neuronové sítě. Pojďme nyní definovat nákladovou funkci.

Nákladová funkce křížové entropie

Mohli bychom vyvinout vlastní vyjádření nákladů na křížovou entropii na základě hodnoty y_. Pak však musíme být opatrní při zacházení s hodnotami NaN. Naštěstí TensorFlow poskytuje šikovnou funkci, která aplikuje soft-max následovaný ztrátou křížové entropie:

cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=dense_layer2, labels=y))

Funkce softmax_cross_entropy_with_logits() má dva argumenty – první ( logits ) je výstup maticového násobení finální vrstvy (plus bias) a druhý je trénovací cílový vektor. Funkce nejprve vezme soft-max násobení matice a poté jej porovná s trénovacím cílem pomocí křížové entropie. Výsledkem je výpočet křížové entropie na trénovací vzorek, takže musíme tento tenzor zredukovat na skalár (jedinou hodnotu). K tomu používáme tf.reduce_mean() , která přebírá střední hodnotu tenzoru.

Trénink konvoluční neuronové sítě

Následující kód je zbytek toho, co je potřeba k trénování sítě. K trénování naší sítě budeme používat minidávky. Základní struktura je:

Vytvořte optimalizátor
Vytvářejte operace správné predikce a vyhodnocování přesnosti
Inicializujte operace
Určete počet dávkových běhů v rámci tréninkové epochy
Pro každou epochu:
- Pro každou dávku:
  - Extrahujte data šarže
  - Spusťte operace optimalizace a křížové entropie
  - Přidejte k průměrným nákladům
- Vypočítejte aktuální přesnost testu
- Vytiskněte si nějaké výsledky
Vypočítejte konečnou přesnost testu a vytiskněte

Kód, který to provede, je:

# add an optimiser
optimiser = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cross_entropy)

# define an accuracy assessment operation
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

# setup the initialisation operator
init_op = tf.global_variables_initializer()

with tf.Session() as sess:
    # initialise the variables
    sess.run(init_op)
    total_batch = int(len(mnist.train.labels) / batch_size)
    for epoch in range(epochs):
        avg_cost = 0
        for i in range(total_batch):
            batch_x, batch_y = mnist.train.next_batch(batch_size=batch_size)
            _, c = sess.run([optimiser, cross_entropy], 
                            feed_dict={x: batch_x, y: batch_y})
            avg_cost += c / total_batch
        test_acc = sess.run(accuracy, 
                       feed_dict={x: mnist.test.images, y: mnist.test.labels})
        print("Epoch:", (epoch + 1), "cost =", "{:.3f}".format(avg_cost), " 
                 test accuracy: {:.3f}".format(test_acc))

    print("\nTraining complete!")
    print(sess.run(accuracy, feed_dict={x: mnist.test.images, y: mnist.test.labels}))

Upozornění: Jedná se o poměrně rozsáhlou síť a na standardním domácím počítači bude pravděpodobně trvat nejméně 10-20 minut, než se spustí.

Výsledky

Spuštění výše uvedeného kódu poskytne následující výstup:

Epoch: 1 cost = 0.739  test accuracy: 0.911
Epoch: 2 cost = 0.169  test accuracy: 0.960
Epoch: 3 cost = 0.100  test accuracy: 0.978
Epoch: 4 cost = 0.074  test accuracy: 0.979
Epoch: 5 cost = 0.057  test accuracy: 0.984
Epoch: 6 cost = 0.047  test accuracy: 0.984
Epoch: 7 cost = 0.040  test accuracy: 0.986
Epoch: 8 cost = 0.034  test accuracy: 0.986
Epoch: 9 cost = 0.029  test accuracy: 0.989
Epoch: 10 cost = 0.025  test accuracy: 0.990

Training complete!
0.9897

Můžeme také vykreslit přesnost testu oproti počtu epoch pomocí TensorBoard (vizualizační sada TensorFlow):

Přesnost konvoluční neuronové sítě MNIST

Jak lze pozorovat, po 10 epochách jsme dosáhli působivé předpovědní přesnosti 99 %. Tohoto výsledku bylo dosaženo bez rozsáhlé optimalizace parametrů konvoluční neuronové sítě a také bez jakékoli formy regularizace. To je ve srovnání s nejlepší přesností, které jsme mohli dosáhnout v naší standardní neuronové síti ~98%.

Rozdíl v přesnosti bude ještě výraznější při srovnání standardních neuronových sítí s konvolučními neuronovými sítěmi na komplikovanějších souborech dat, jako jsou data CIFAR. To je však téma na jiný den. Bavte se používáním TensorFlow a konvolučních neuronových sítí! Mimochodem, pokud chcete vidět, jak vytvořit neuronovou síť v Kerasu, efektivnějším frameworku, podívejte Keras tutoriál.

import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data


def run_cnn():
    mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

    # Python optimisation variables
    learning_rate = 0.0001
    epochs = 10
    batch_size = 50

    # declare the training data placeholders
    # input x - for 28 x 28 pixels = 784 - this is the flattened image data that is drawn from mnist.train.nextbatch()
    x = tf.placeholder(tf.float32, [None, 784])
    # reshape the input data so that it is a 4D tensor.  The first value (-1) tells function to dynamically shape that
    # dimension based on the amount of data passed to it.  The two middle dimensions are set to the image size (i.e. 28
    # x 28).  The final dimension is 1 as there is only a single colour channel i.e. grayscale.  If this was RGB, this
    # dimension would be 3
    x_shaped = tf.reshape(x, [-1, 28, 28, 1])
    # now declare the output data placeholder - 10 digits
    y = tf.placeholder(tf.float32, [None, 10])

    # create some convolutional layers
    layer1 = create_new_conv_layer(x_shaped, 1, 32, [5, 5], [2, 2], name='layer1')
    layer2 = create_new_conv_layer(layer1, 32, 64, [5, 5], [2, 2], name='layer2')

    # flatten the output ready for the fully connected output stage - after two layers of stride 2 pooling, we go
    # from 28 x 28, to 14 x 14 to 7 x 7 x,y co-ordinates, but with 64 output channels.  To create the fully connected,
    # "dense" layer, the new shape needs to be [-1, 7 x 7 x 64]
    flattened = tf.reshape(layer2, [-1, 7 * 7 * 64])

    # setup some weights and bias values for this layer, then activate with ReLU
    wd1 = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1000], stddev=0.03), name='wd1')
    bd1 = tf.Variable(tf.truncated_normal([1000], stddev=0.01), name='bd1')
    dense_layer1 = tf.matmul(flattened, wd1) + bd1
    dense_layer1 = tf.nn.relu(dense_layer1)

    # another layer with softmax activations
    wd2 = tf.Variable(tf.truncated_normal([1000, 10], stddev=0.03), name='wd2')
    bd2 = tf.Variable(tf.truncated_normal([10], stddev=0.01), name='bd2')
    dense_layer2 = tf.matmul(dense_layer1, wd2) + bd2
    y_ = tf.nn.softmax(dense_layer2)

    cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=dense_layer2, labels=y))

    # add an optimiser
    optimiser = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cross_entropy)

    # define an accuracy assessment operation
    correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

    # setup the initialisation operator
    init_op = tf.global_variables_initializer()

    # setup recording variables
    # add a summary to store the accuracy
    tf.summary.scalar('accuracy', accuracy)

    merged = tf.summary.merge_all()
    writer = tf.summary.FileWriter('C:\\Users\\PycharmProjects')
    with tf.Session() as sess:
        # initialise the variables
        sess.run(init_op)
        total_batch = int(len(mnist.train.labels) / batch_size)
        for epoch in range(epochs):
            avg_cost = 0
            for i in range(total_batch):
                batch_x, batch_y = mnist.train.next_batch(batch_size=batch_size)
                _, c = sess.run([optimiser, cross_entropy], feed_dict={x: batch_x, y: batch_y})
                avg_cost += c / total_batch
            test_acc = sess.run(accuracy, feed_dict={x: mnist.test.images, y: mnist.test.labels})
            print("Epoch:", (epoch + 1), "cost =", "{:.3f}".format(avg_cost), " test accuracy: {:.3f}".format(test_acc))
            summary = sess.run(merged, feed_dict={x: mnist.test.images, y: mnist.test.labels})
            writer.add_summary(summary, epoch)

        print("\nTraining complete!")
        writer.add_graph(sess.graph)
        print(sess.run(accuracy, feed_dict={x: mnist.test.images, y: mnist.test.labels}))


def create_new_conv_layer(input_data, num_input_channels, num_filters, filter_shape, pool_shape, name):
    # setup the filter input shape for tf.nn.conv_2d
    conv_filt_shape = [filter_shape[0], filter_shape[1], num_input_channels, num_filters]

    # initialise weights and bias for the filter
    weights = tf.Variable(tf.truncated_normal(conv_filt_shape, stddev=0.03), name=name+'_W')
    bias = tf.Variable(tf.truncated_normal([num_filters]), name=name+'_b')

    # setup the convolutional layer operation
    out_layer = tf.nn.conv2d(input_data, weights, [1, 1, 1, 1], padding='SAME')

    # add the bias
    out_layer += bias

    # apply a ReLU non-linear activation
    out_layer = tf.nn.relu(out_layer)

    # now perform max pooling
    # ksize is the argument which defines the size of the max pooling window (i.e. the area over which the maximum is
    # calculated).  It must be 4D to match the convolution - in this case, for each image we want to use a 2 x 2 area
    # applied to each channel
    ksize = [1, pool_shape[0], pool_shape[1], 1]
    # strides defines how the max pooling area moves through the image - a stride of 2 in the x direction will lead to
    # max pooling areas starting at x=0, x=2, x=4 etc. through your image.  If the stride is 1, we will get max pooling
    # overlapping previous max pooling areas (and no reduction in the number of parameters).  In this case, we want
    # to do strides of 2 in the x and y directions.
    strides = [1, 2, 2, 1]
    out_layer = tf.nn.max_pool(out_layer, ksize=ksize, strides=strides, padding='SAME')

    return out_layer

if __name__ == "__main__":
    run_cnn()

Učení konvolučních neuronových sítí v TensorFlow